Angles in radians and degrees

January 26, 2026

This is not a math tutorial. See Why am I writing about math?

Taking the point (2, 2) as an example:

(2, 2) in degrees is $45^\circ$
(2, 2) in radians is $\pi/4 \approx 0.785$ radians

The conversion is:

$360^\circ = 2 \pi \text{ radians}$
$180^\circ = \pi\text{ radians}$
$90^\circ = \pi/2\text{ radians}$
$45^\circ = \pi/4\text{ radians}$
…

**Radians measure angles in terms of $\pi$ .

The arctan2 function #

The arctangent function is the inverse of the tangent function. It is used to find the angle of the tangent.

The tan function #

Remember that tangent = opposite/adjacent (TOA).

Remember to always pass angles to trig functions, not the result of other trig functions. For example, considering the point (2, 2), the angle is $\pi/4$ . $\tan(\pi/4) = 1.0$

The relationship between tan and arctan #

tan goes from angle -> slope (opposite/adjacent); atan goes from slope -> angle

Python example:

In [101]: angle_from_slope_45 == np.pi/4
Out[101]: np.True_

In [102]: slope_45 = np.tan(np.pi/4)

In [103]: angle_from_slope_45 = (np.arctan(slope_45))

In [104]: angle_from_slope_45 == np.pi/4
Out[104]: np.True_

arctan2 versus arctan #

The following example illustrates the difference between arctan2 and arctan:

In [105]: x = -2

In [106]: y = -2

In [107]: np.arctan(y/x)
Out[107]: np.float64(0.7853981633974483)

In [108]: np.arctan2(y, x)
Out[108]: np.float64(-2.356194490192345)

atan (or arctan) takes a single number (the slope y/x, opposite/adjacent). It can only return angles between $-\pi/2$ and $\pi/2$ (the right side of the circle).

atan2 (or arctan2) takes 2 arguments (y, x). It returns angles in the full range of the circle ( $-\pi$ to $pi$ ). The takeaway is to use atan2.

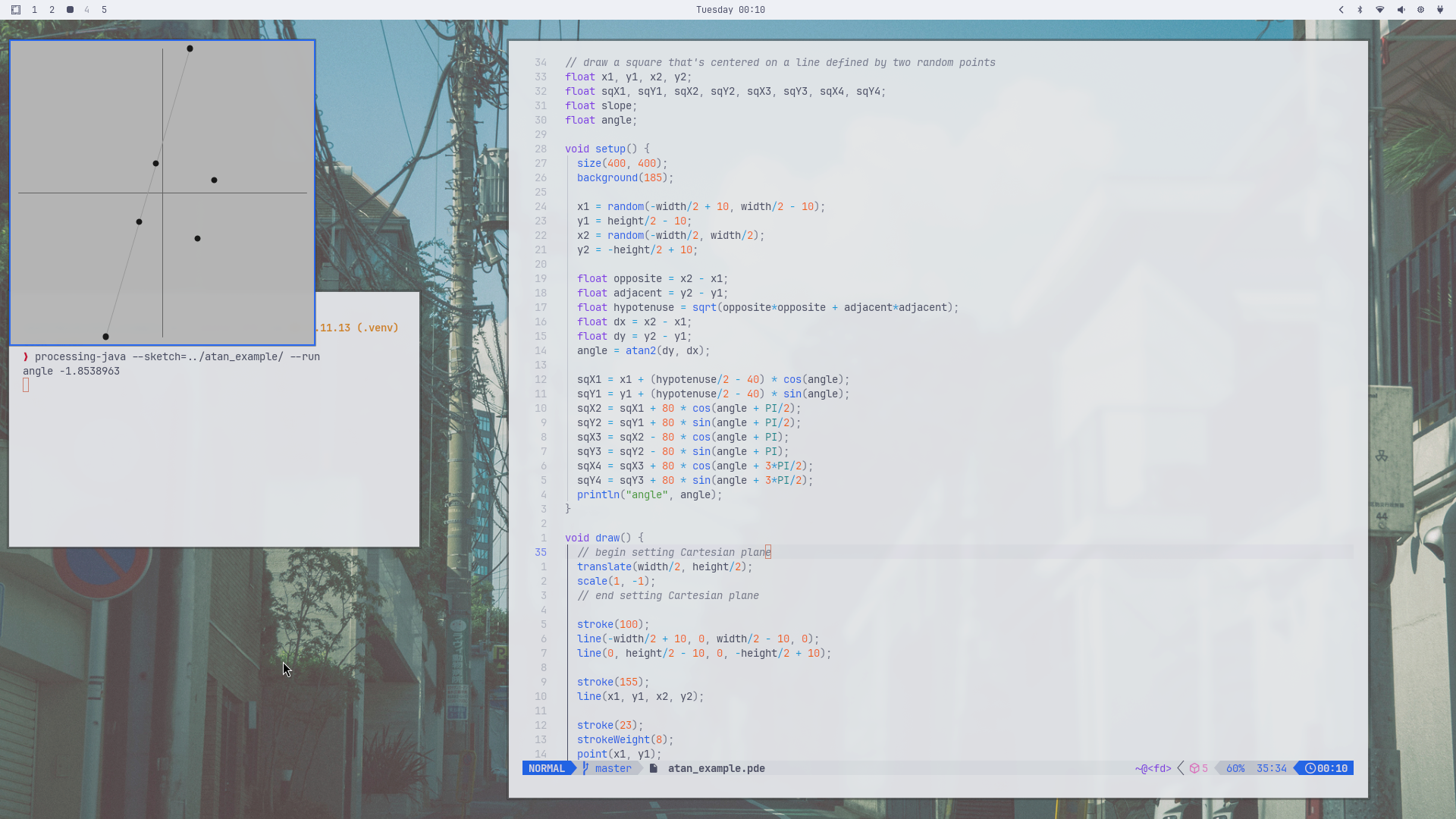
An example using atan2 in a Processing sketch #

A square that aligns with two random points:

// draw a square that's centered on a line defined by two random points
float x1, y1, x2, y2;
float sqX1, sqY1, sqX2, sqY2, sqX3, sqY3, sqX4, sqY4;
float slope;
float angle;

void setup() {
  size(400, 400);
  background(185);

  x1 = random(-width/2 + 10, width/2 - 10);
  y1 = height/2 - 10;
  x2 = random(-width/2, width/2);
  y2 = -height/2 + 10;

  float opposite = x2 - x1;
  float adjacent = y2 - y1;
  float hypotenuse = sqrt(opposite*opposite + adjacent*adjacent);
  float dx = x2 - x1;
  float dy = y2 - y1;
  angle = atan2(dy, dx);

  sqX1 = x1 + (hypotenuse/2 - 40) * cos(angle);
  sqY1 = y1 + (hypotenuse/2 - 40) * sin(angle);
  sqX2 = sqX1 + 80 * cos(angle + PI/2);
  sqY2 = sqY1 + 80 * sin(angle + PI/2);
  sqX3 = sqX2 - 80 * cos(angle + PI);
  sqY3 = sqY2 - 80 * sin(angle + PI);
  sqX4 = sqX3 + 80 * cos(angle + 3*PI/2);
  sqY4 = sqY3 + 80 * sin(angle + 3*PI/2);
  println("angle", angle);
}

void draw() {
  // begin setting Cartesian plane
  translate(width/2, height/2);
  scale(1, -1);
  // end setting Cartesian plane

  stroke(100);
  line(-width/2 + 10, 0, width/2 - 10, 0);
  line(0, height/2 - 10, 0, -height/2 + 10);

  stroke(155);
  line(x1, y1, x2, y2);

  stroke(23);
  strokeWeight(8);
  point(x1, y1);
  point(x2, y2);

  point(sqX1, sqY1);
  point(sqX2, sqY2);
  point(sqX3, sqY3);
  point(sqX4, sqY4);

  noLoop();
}

Points, vectors, and angles #

For the case of finding the angle of point x2, y2 in relation to point x1, y1, I’ve struggled to understand what the angle that’s calculated is the angle of. One way to make that clear is to think of it in terms of translating the origin of the graph to point x1, y1. That makes it clear that the angle is the angle relative to the positive x-axis of the translated origin.

I’ve also wondered about the meaning of dx, dy (“delta x”, “delta y”). For example:

int x1 = -183;
int y1 = 190;
int x2 = 107;
int y2 = -30;

int dx = x2 - x1;
int dy = y2 - y1;

dx, dy is a point and a “vector”.

A point is a specific location in space: x1, y1, dx, dy, etc. A vector is a displacement or direction with a magnitude: “move 3 units to the right, 5 units down”. A vector doesn’t have a specific location in space.

dx, dy can be plotted as a point, as it is in the image below. It also defines a vector. When atan2 is used to calculate the angle of point x2, y2 in relation to point x1, y1 with:

float slope = atan2(dy, dx);

it’s essentially asking “what angle does the vector from the origin to the point(dx, dy) make with the positive x-axis?”

This code was used to generate the image above:

size(600, 600);
textSize(16);

int hW = width/2;
int hH = height/2;

// translate and scale the window into the Cartesian coordinate system
translate(hW, hH);
scale(1, -1);

int x1 = -183;
int y1 = 190;
int x2 = 107;
int y2 = -30;

int dx = x2 - x1;
int dy = y2 - y1;

stroke(155);
line(-hW, 0, hW, 0);
line(0, hH, 0, -hH);
line(0, 0, dx, dy);
strokeWeight(8);
point(0, 0);
point(dx, dy);

stroke(158, 13, 59);
strokeWeight(8);
point(x1, y1);
strokeWeight(1);
line(x1, -hH, x1, hH);
line(-hW, y1, hW, y1);

stroke(5, 153, 34);
strokeWeight(8);
point(x2, y2);
strokeWeight(1);
line(x2, -hH, x2, hH);
line(-hW, y2, hW, y2);

float angle = atan2(dy, dx);

float xI1 = x1 + 150 * cos(angle);
float yI1 = y1 + 150 * sin(angle);

stroke(173, 138, 40);
strokeWeight(8);
point(xI1, yI1);
strokeWeight(1);
line(x1, y1, xI1, yI1);

float xI2 = x2 + 150 * cos(angle);
float yI2 = y2 + 150 * sin(angle);

stroke(222, 75, 205);
strokeWeight(8);
point(xI2, yI2);
strokeWeight(1);
line(x2, y2, xI2, yI2);
point(dx, dy);

pushMatrix();
scale(1, -1);  // compensate for the reversed y-axis
fill(45);
text("\u03B8 = " + angle, x1 + 28, -y1 + 20);
text("\u03B8 = " + angle, x2 + 28, -y2 + 20);
text("\u03B8 = " + angle, 0 + 28, 20);
text("(dx: "+ dx + ",dy: " + dy + ")", dx - 110, -dy - 6);
popMatrix();

// save("slope_angle_example.png");

Tags: