Finding roots with Newton's method
This is not a math tutorial. See Why am I writing about math?
The root, or zero of a function is any input value that makes the function’s output equal to zero, i.e., . Roots are the points where the function’s graph crosses or touches the horizontal x-axis.
What is Newton’s Method? #
Following this video, for no particular reason (haven’t watched it yet. Edit, it turned out to be too fast for me.):
-
pick an x close to the root of a continuous function
-
take the derivative of to get
-
plug those values into this formula:
-
repeat until the result converges, i.e., where
Example, find the root of:
Let’s make it real with Python:
import numpy as np
import matplotlib.pyplot as plt
def sin_cos_exp(x):
return np.sin(np.cos(np.exp(x)))
x_arr = np.linspace(-2, 2, 100)
y_arr = [sin_cos_exp(x) for x in x_arr]
plt.plot(x_arr, y_arr)
plt.axhline(y=0, color="k", linewidth=0.5)
plt.axvline(x=0, color="k", linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.show()
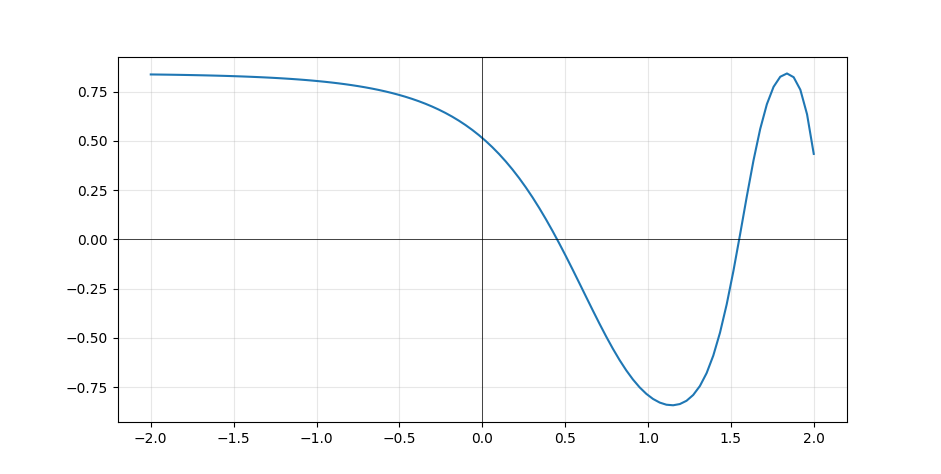
sin(cos(e^x))
The graph is showing that the function will return a value of 0 when it’s called with values that are approximately 0.4 and 1.5. Newton’s method can be used to find a root (an argument that will cause the function to cross or touch the 0 line), by repeatedly calling:
x_next = x_current - (f(x_current) / f'(x_current))
Where x_current is the value that was previously assigned to x_next. Note that I’m using f'(x_current) to mean
the derivative of the function with respect to x_current.
For my own reference, this can be made clearer with Python code:
import numpy as np
def sin_cos_exp(x):
return np.sin(np.cos(np.exp(x)))
# finding the derivative of f(x) = sin(cos(e^x))
# Note that:
# d/dx[sin(x)] = cos(x)
# d/dx[cos(x)] = -sin(x)
# d/dx[e^x] = e^x
# think of it as three nested functions:
# sin(u) where u = cos(e^x); d/dx[sin(cos(e^x))] = cos(cos(e^x)) x d/dx[cos(e^x)]
# cos(v) where v = e^x; d/dx[cos(e^x)] = -sin(e^x) x d/dx[e^x]
# innermost e^x; d/dx[e^x] = e^x; (the derivative of e^x is e^x)
# f'(x) = cos(cos(e^x)) x -sin(e^x) x e^x
def sin_cos_exp_derivatives(x):
expx = np.exp(x)
return np.cos(np.cos(expx)) * -np.sin(expx) * expx
print("x=0.0", sin_cos_exp_derivatives(0.0))
# x=0.0 -0.7216061490634433
print("x=0.4", sin_cos_exp_derivatives(0.4))
# x=0.4 -1.4825498531537413
With the sin_cos_exp and sin_cos_exp_derivatives functions, it’s possible to write a
newtons_method function:
def newtons_method(x0, tolerance=1e-6, max_iter=100):
xn = x0
for n in range(max_iter):
fxn = sin_cos_exp(xn)
if abs(fxn) < tolerance:
print(f"Found solution {xn} after {n} iterations.")
return xn
dfxn = sin_cos_exp_derivatives(xn)
if dfxn == 0:
print("Zero derivative. No solution found.")
return None
xn = xn - fxn / dfxn
print("Exceeded max iterations. No solution found.")
return None
newtons_method(0.4)
newtons_method(1.5)
Calling that function returns:
Found solution 0.45158270529021377 after 3 iterations.
Found solution 1.5501949939676198 after 3 iterations.
Since it’s a periodic function, there are an infinite number of zero crossings:
{{x< figure src="/images/sin_cos_exp_periods.png" >}}
Finding square roots via Newton’s Method #
Find the zero for:
Where a is the value we want to get the square root of.
Confirm that makes sense:
The reasoning is that when f(x) = 0 then x^2 = a and x = sqrt(a)
The derivative of f(x) = x^2 is:
Having the derivative, plug the formulas into:
This can be simplified to (NO, IT CAN’T! Be careful about Youtube math tutorials, it should be + a, not - a):
Newton’s formula can be simplified to:1
The simplification isn’t obvious to me. I’ll work it out below, using x instead of x_n to
clarify what’s going on:
Starting from:
Multiply x by 2x/2x (essentially 1) to express everything with a common denominator:
Simplify to:
Combine the fractions:
Simplifies to:
This can be expressed as:
The first term can be simplified, giving:
Then factor out the 1/2:
Using x_n instead, so that it’s expressed in the correct form for Newton’s method:
Intuitive explanation of Newton’s Method for square roots #
Multiplying (x_n + a/x_n) by 1/2 is the same as calculating the average of x_n and a/x_n.
If x_n is too big, then a/x_n will be too small (less than the square root of a), and the
average of x_n and a/x_n will be closer to the square root of a. And vice versa.
Python demo:
In [22]: a = 9
In [23]: x = 1
In [24]: x = 0.5 * (x + a/x)
In [25]: x
Out[25]: 5.0
In [26]: x = 0.5 * (x + a/x)
In [27]: x
Out[27]: 3.4
In [28]: x = 0.5 * (x + a/x)
In [29]: x
Out[29]: 3.023529411764706
In [30]: x = 0.5 * (x + a/x)
In [31]: x
Out[31]: 3.00009155413138
Calculating the square root of 2 from an initial estimate of 1:
In [32]: a = 2
In [33]: x = 1
In [34]: x = 0.5 * (x + a/x)
In [35]: x
Out[35]: 1.5
In [36]: x = 0.5 * (x + a/x)
In [37]: x
Out[37]: 1.4166666666666665
In [38]: x = 0.5 * (x + a/x)
In [39]: x
Out[39]: 1.4142156862745097
In [40]: x = 0.5 * (x + a/x)
In [41]: x
Out[41]: 1.4142135623746899
In [42]: x = 0.5 * (x + a/x)
In [43]: x
Out[43]: 1.414213562373095
References #
Johnson, S. G. “Square Roots via Newton’s Method”. MIT Course 18.335. https://math.mit.edu/~stevenj/18.335/newton-sqrt.pdf .
Notes #
-
S. G. Johnson, “Square Roots via Newton’s Method”, MIT Course 18.3335, February 4, 2015, p.1, https://math.mit.edu/~stevenj/18.335/newton-sqrt.pdf ↩︎