Generating fractals with Halley's method
A dump of images and code.
Images #

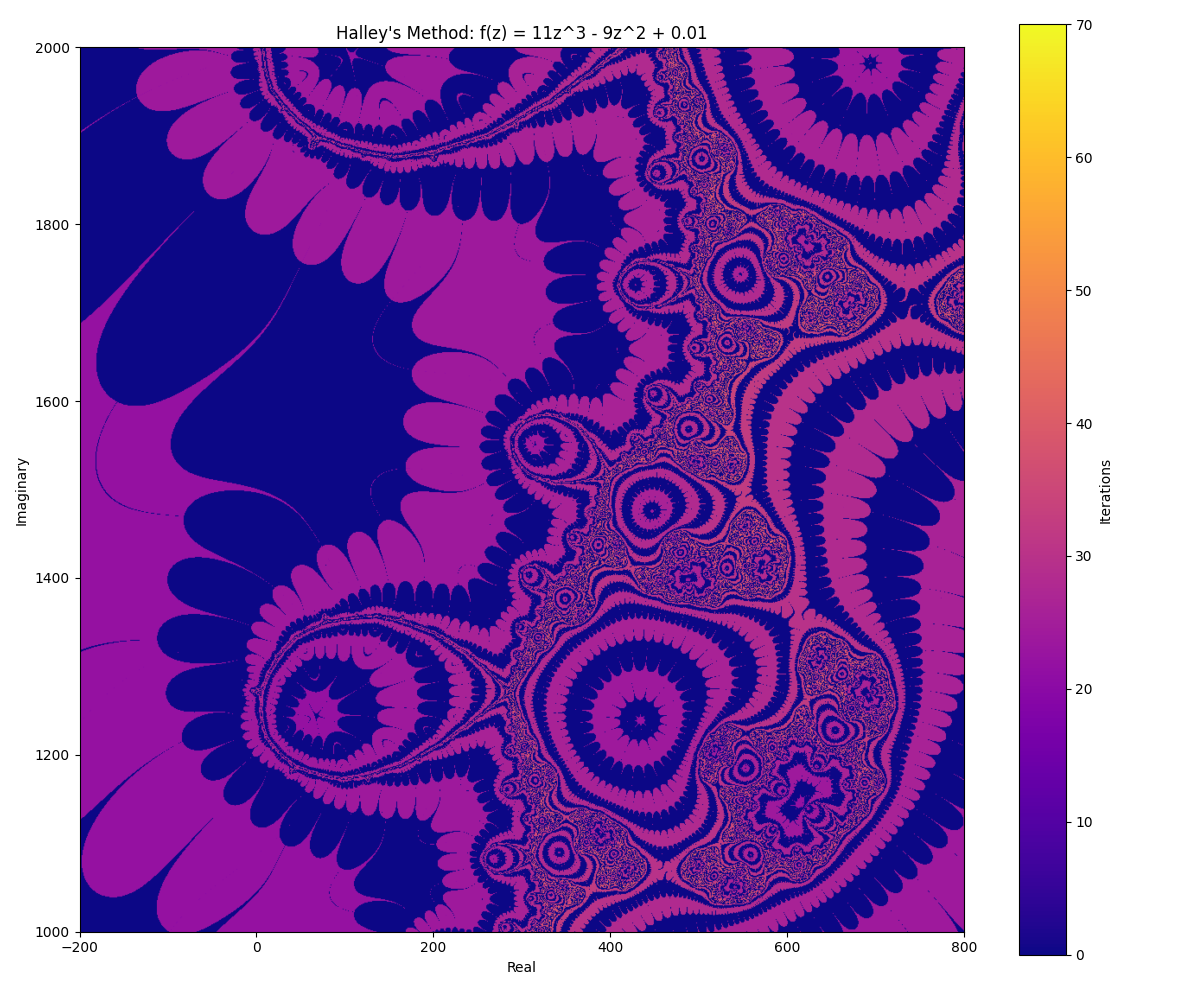
Code #
import numpy as np
import matplotlib.pyplot as plt
def halley_fractal(
f,
df,
ddf,
roots,
width=800,
height=800,
xmin=-2,
xmax=2,
ymin=-2,
ymax=2,
max_iter=50,
):
"""
Generate a fractal using Halley's method.
Returns:
image array
"""
# create a grid of complex numbers
x = np.linspace(xmin, xmax, width)
y = np.linspace(ymin, ymax, height)
X, Y = np.meshgrid(x, y)
Z = X + 1j * Y # treat each coordinate as a complex number
# arrays to store results
root_map = np.zeros((height, width), dtype=int)
iter_map = np.zeros((height, width), dtype=int)
# apply halleys method to each point
for i in range(height):
for j in range(width):
z = Z[i, j]
for iteration in range(max_iter):
fz = f(z)
dfz = df(z)
ddfz = ddf(z)
# check for convergence
if abs(fz) < 1e-6:
# determine which root z has converged to
distances = [abs(z - root) for root in roots]
root_idx = np.argmin(distances)
root_map[i, j] = root_idx
iter_map[i, j] = iteration
break
# Halley's formula
denominator = 2 * dfz**2 - fz * ddfz
if abs(denominator) < 1e-15:
break
z = z - (2 * fz * dfz) / denominator
else:
# didn't converge
root_map[i, j] = -1
iter_map[i, j] = max_iter
return root_map, iter_map
# f(z) = z^3 - 1
# def f(z):
# return z**3 - 1
# def df(z):
# return 3 * z**2
# def ddf(z):
# return 6 * z
# the three cube roots of 1
roots = [1, np.exp(2j * np.pi / 3), np.exp(4j * np.pi / 3)]
# roots [1, np.complex128(-0.4999999999999998+0.8660254037844387j), np.complex128(-0.5000000000000004-0.8660254037844384j)]
# max_iter = 100
# root_map, iter_map = halley_fractal(f, df, ddf, roots, max_iter=max_iter)
#
# # visualize
# fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
#
# # show which root each point converges to
# im1 = ax1.imshow(root_map, extent=[-2, 2, -2, 2], cmap="tab10", origin="lower")
# ax1.set_title("Basins of Attraction")
# ax1.set_xlabel("Real")
# ax1.set_ylabel("Imaginary")
#
#
# # Show convergence speed (with color based on root)
# # Combine root and iteration info for more interesting coloring
# combined = root_map * max_iter + iter_map
# im2 = ax2.imshow(combined, extent=[-2, 2, -2, 2], cmap="hot", origin="lower")
# ax2.set_title("Convergence Speed")
# ax2.set_xlabel("Real")
# ax2.set_ylabel("Imaginary")
#
# plt.tight_layout()
# plt.show()
# Halley's fractal single root (Claude's attempt to convert Michael Levin's Matlab code to python)
def halley_convergence_fractal(
f,
df,
ddf,
width=1024,
height=1024,
xmin=-5.0,
xmax=1.0,
ymin=-7.0,
ymax=-2.5,
max_iter=50,
# epsilon=1e-5,
epsilon=1e-6,
):
"""
Generate a Halley's method fractal based on convergence rate.
"""
# Create grid of complex numbers
x = np.linspace(xmin, xmax, width)
y = np.linspace(ymin, ymax, height)
X, Y = np.meshgrid(x, y)
Z = X + 1j * Y
# Arrays to store results
iter_map = np.zeros((height, width), dtype=int)
# Apply Halley's method to each point
for i in range(height):
for j in range(width):
z = Z[i, j]
# g_prev = abs(z) ** 2 # Note: this is weird, doesn't get used due to the (correct) K > 1 condition
g_prev = None # initializing to None; doesn't get used unitl K > 1
for k in range(1, max_iter + 1):
fz = f(z)
dfz = df(z)
ddfz = ddf(z)
# Halley's formula
denominator = 2 * dfz**2 - fz * ddfz
if abs(denominator) < 1e-15:
break
z = z - (2 * fz * dfz) / denominator
# Check convergence
g = abs(z) ** 2
if k > 1 and abs(g - g_prev) < epsilon:
# Converged - store iteration count
if (
k % 2 == 0
): # this is in the original code and seems to produce more intersting patterns
iter_map[i, j] = k
break
g_prev = g
return iter_map, x, y
# Functions
# def f(z):
# return z**2 + 0.001
#
#
# def df(z):
# return 2 * z
#
#
# # z isnt' accessed, but it's convenient to keep in in the function signature
# def ddf(z):
# return 2
# def f(z):
# return z**9 - 1
#
#
# def df(z):
# return 9 * z**8
#
#
# def ddf(z):
# return 72 * z**7
# def f(z):
# return z**8 + 3 * z - 0.01
#
#
# def df(z):
# return 8 * z**7 + 3
#
#
# def ddf(z):
# return 56 * z**6
# the general pattern
# f(x) = 3x^5 + 2x^3 - 1
# f'(x) = 15x^4 + 6x^2
# f''(x) = 60x^3 + 12x
def f(z):
return 3 * z**5 - 3.7 * z**3 - 0.002
def df(z):
return 15 * z**4 - 3.7 * 3 * z**2
def ddf(z):
return 60 * z**3 - 3.7 * 3 * 2 * z
# Generate fractal with Levin's parameters
print("Generating fractal...")
result, xs, ys = halley_convergence_fractal(
f,
df,
ddf,
width=1024,
height=1024,
xmin=-1000,
xmax=1000,
ymin=100,
ymax=2100,
max_iter=300,
)
# Visualize
plt.figure(figsize=(12, 10))
plt.imshow(
result,
extent=(xs[0], xs[-1], ys[0], ys[-1]),
# cmap="hot",
cmap="tab20c",
origin="lower",
interpolation="bilinear",
)
plt.title("Halley's Method: f(z) = 3z^5 + 2z^3 -0.001")
plt.xlabel("Real")
plt.ylabel("Imaginary")
plt.colorbar(label="Iterations")
plt.tight_layout()
plt.show()
print(f"Iteration range: {result.min()} to {result.max()}")
print(f"Non-zero pixels: {np.count_nonzero(result)}/{result.size}")
References #
Levin, M. “Platonic space: where cognitive and morphological patterns come from (besides genetics and the environment)”. March 9, 2025. https://thoughtforms.life/platonic-space-where-cognitive-and-morphological-patterns-come-from-besides-genetics-and-environment/
Levin, M. “Halley’s Method fractal art”. October 3, 2023. https://thoughtforms.life/halleys-method-fractal-art/
Tags: