Halley's method
This is not a math tutorial. See Why am I writing about math?
Halley’s method is a root-finding algorithm used for functions of one real variable with a continuous second derivative. It’s used for solving the nonlinear equation . The method consists of a sequence of iterations1:
Beginning with an initial guess .
The iteration function is:
Explanation of : it’s a second derivative, or second order derivative. is the derivative of the derivative of .
What’s the significance of the continuous second derivative condition? It means that the rate of change of the slope doesn’t have any sudden jumps, i.e., that it’s continuous.
Finding the square root with Halley’s Method #
For reference, see the note on notes / Newton’s Method. This function is the key:
Where is the number you want to get the square root for. Essentially, the square root of some number squared, minus the number, will equal zero. Halley’s Method is used to find the value of that results in .
Here’s a Python implementation. It works for real and complex numbers:
def halley_method(f, df, ddf, x0, tol=1e-10, max_iter=100):
"""
Find root using Halley's method.
Args:
f: function
df: first derivative
ddf: second derivative
x0: initial guess
max_iter: maximum iterations
Returns:
The approximate root
"""
x = x0
for i in range(max_iter):
fx = f(x)
dfx = df(x)
ddfx = ddf(x)
# note: for complex numbers `abs()` returns the magnitude (distance from origin) in the complex plane
if abs(fx) < tol:
print(f"Root: {x}, Converged in {i} iterations")
return x
# Halley's formula
denominator = 2 * dfx**2 - fx * ddfx
if abs(denominator) < 1e-15:
print("Denominator too small, stopping")
return x
x_new = x - (2 * fx * dfx) / denominator
print(f"Iteration {i}: x = {x_new:.10f}, f(x) = {f(x_new):.2e}")
x = x_new
print("Max iterations reached")
return x
# x0 = 4
x0 = 2 + 2j
# functions for sqrt(2)
def f(x):
return x**2 - x0 # x^2 - a
# first derivative
def df(x):
return 2 * x
# second derivative
def ddf(x): # x isn't accessed, but the pattern might be useful for other formulas
return 2
root = halley_method(f, df, ddf, x0=x0)
print(f"Approximate root: {root}")
print(f"Actual root: {x0**0.5}")
Returns:
Iteration 0: x = 1.4823529412+0.7294117647j, f(x) = -3.35e-01+1.62e-01j
Iteration 1: x = 1.5538919490+0.6435485026j, f(x) = 4.26e-04+9.67e-06j
Iteration 2: x = 1.5537739740+0.6435942529j, f(x) = 4.13e-14-6.01e-13j
Root: (1.5537739740299803+0.6435942529054128j), Converged in 3 iterations
Approximate root: (1.5537739740299803+0.6435942529054128j)
Actual root: (1.5537739740300374+0.6435942529055827j)
Note that the halley_method function in the above code will work to find the root(s) of other
functions.
Generating fractal art with Halley’s Method #
Inspired by reading Halley’s Method fractal art :
Fractal art can be made by testing each point (x,y) in a region of the complex numbers plane to see how soon a given function (in complex numbers) converges on its root, when using the number x+yi as the starting point of a root-finding method. The rate at which it settles on a root determines the color.2
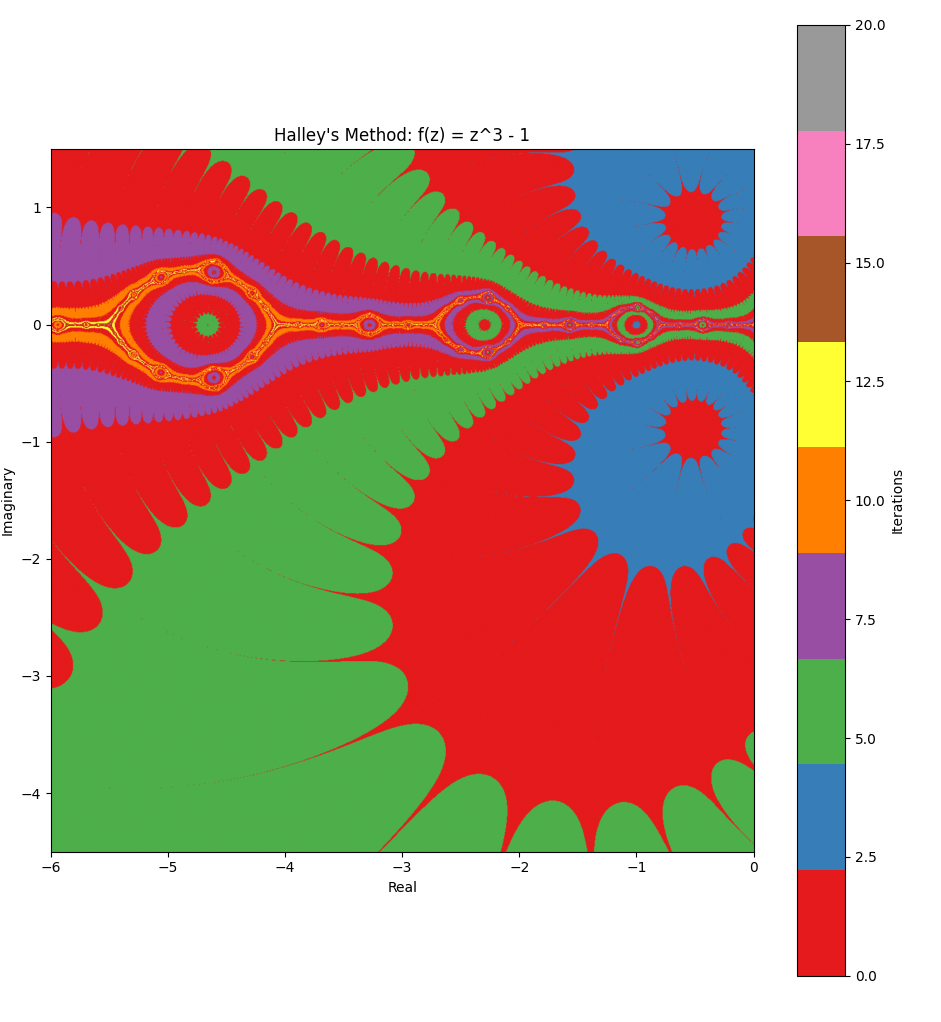
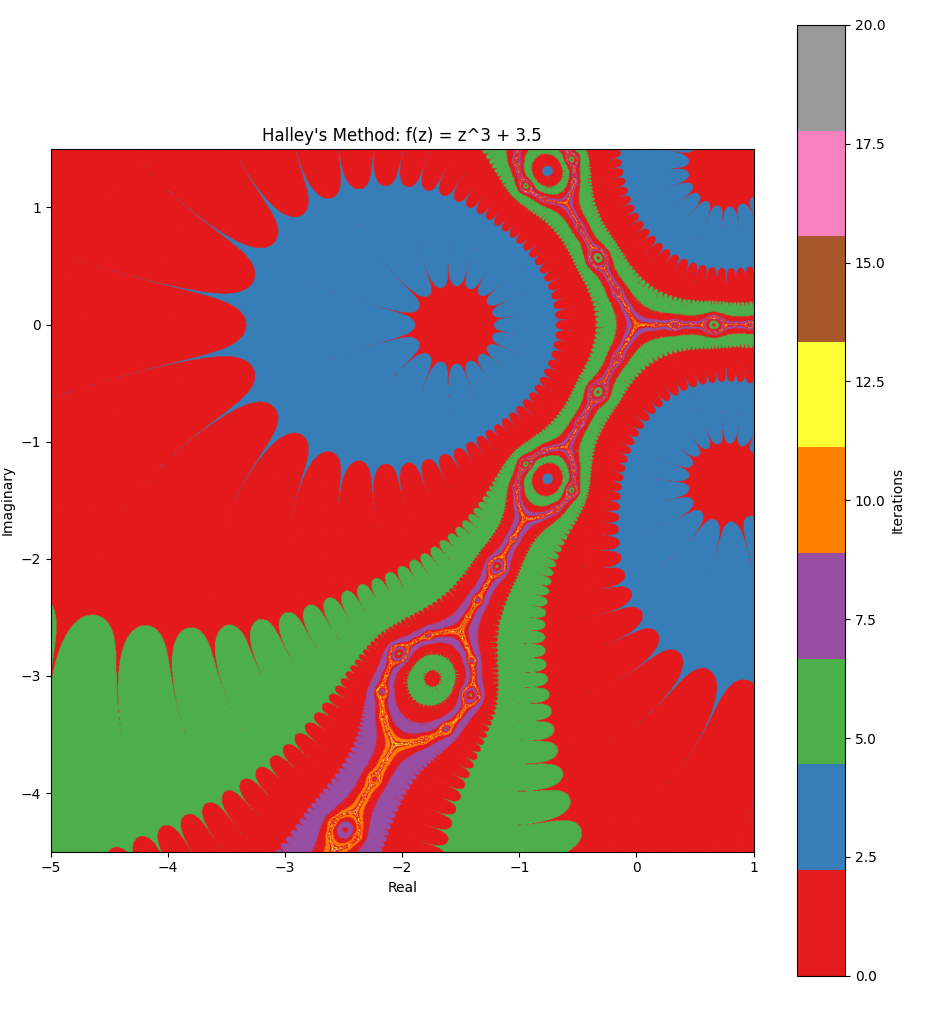
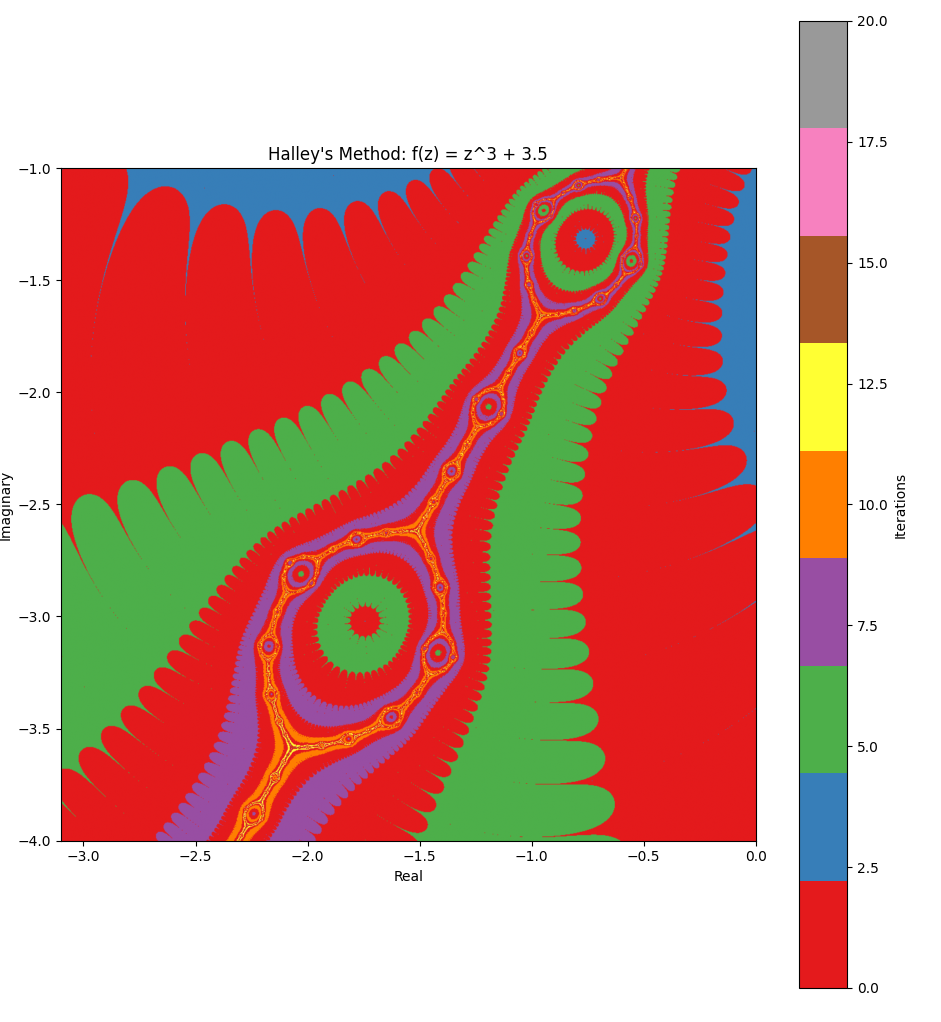
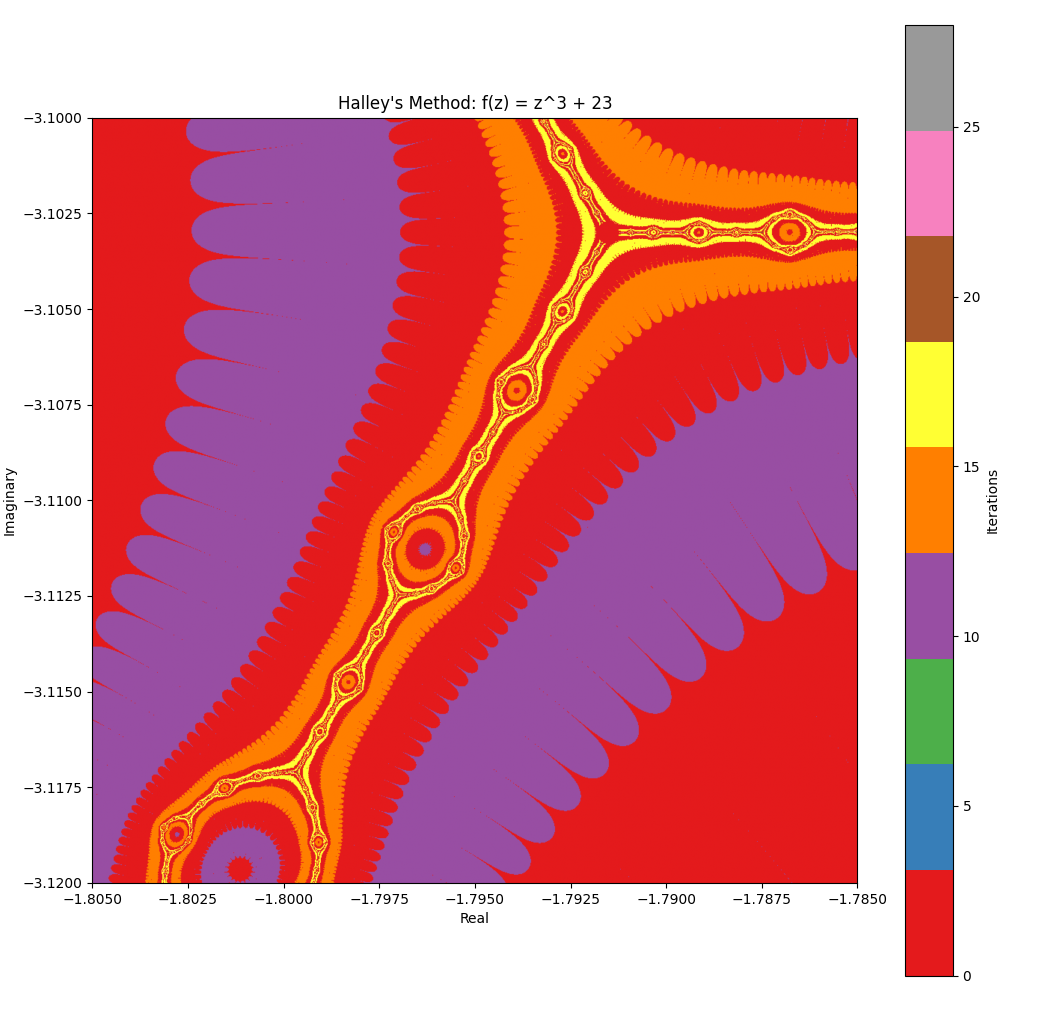
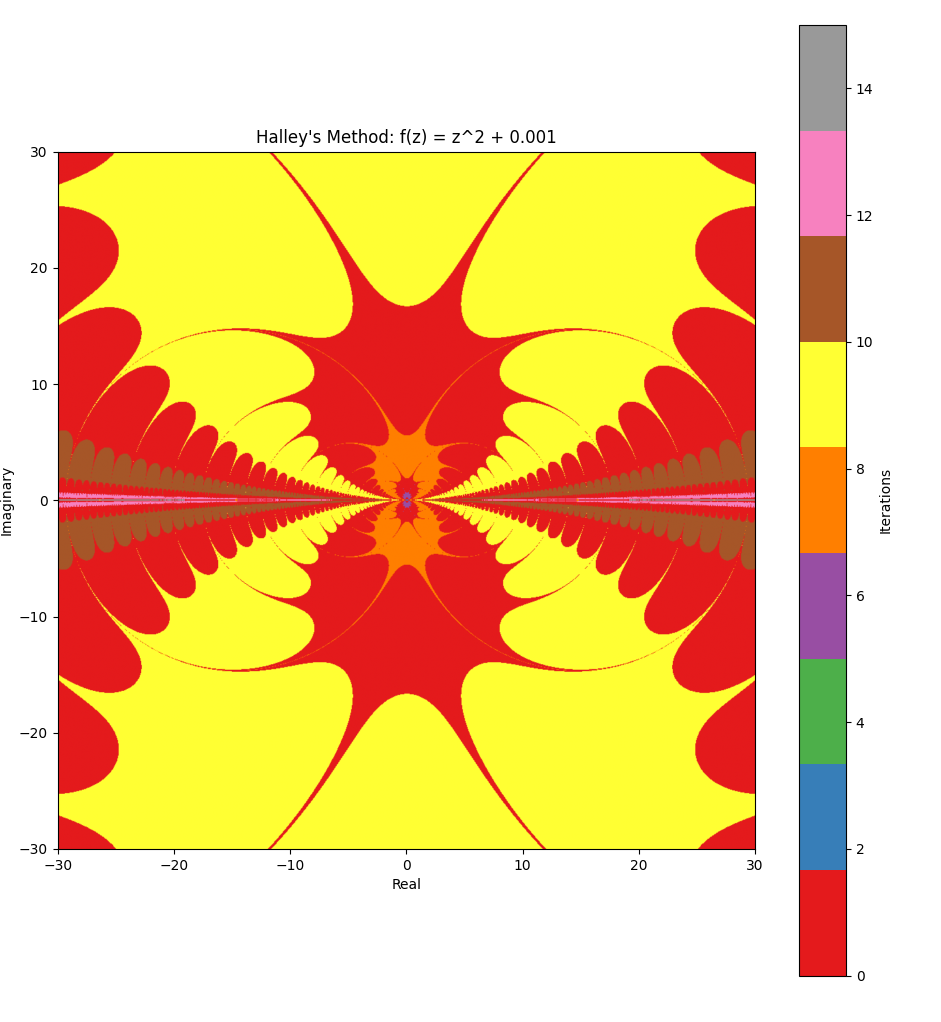
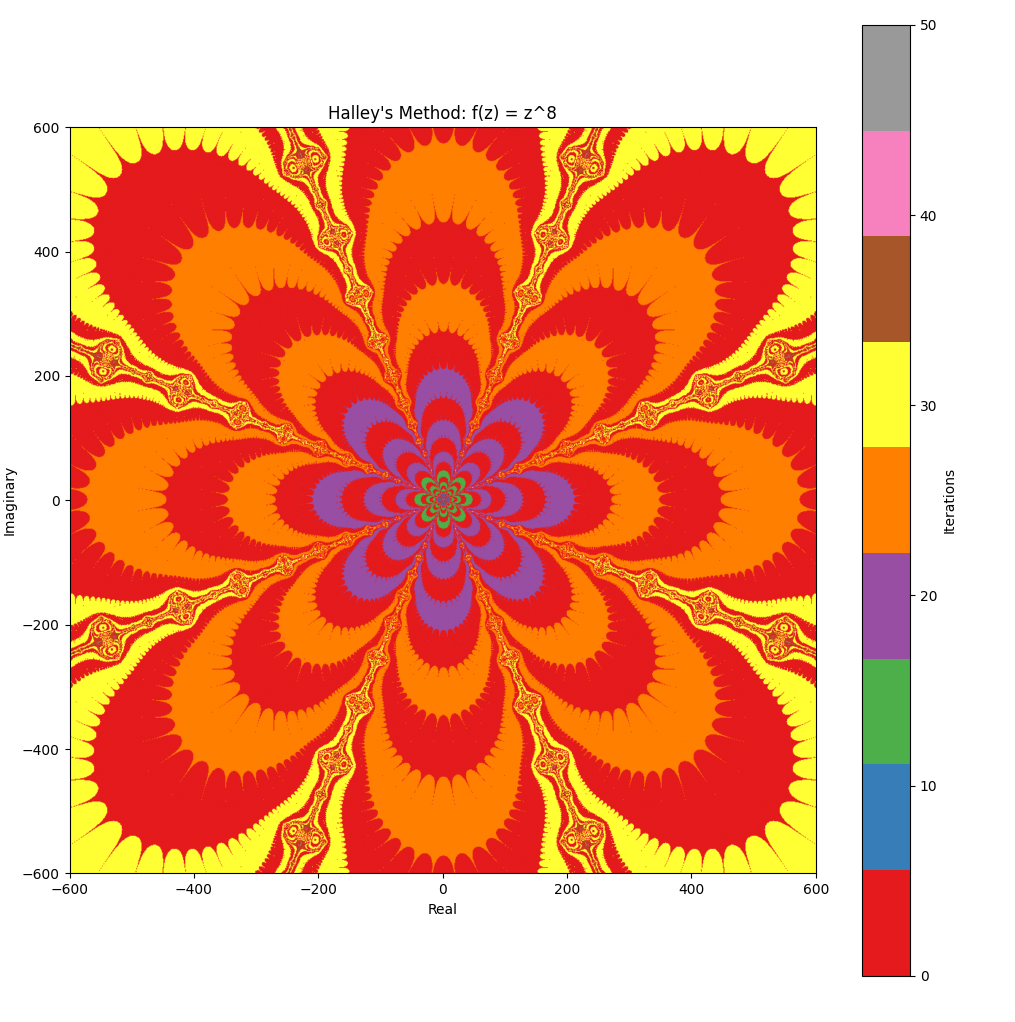
Related #
References #
Wikipedia contributors. “Halley’s method.” Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/w/index.php?title=Halley%27s_method&oldid=1320586249 (accessed December 9, 2025).
Weisstein, Eric W. “Halley’s Method.” From MathWorld–A Wolfram Resource. https://mathworld.wolfram.com/HalleysMethod.html
Notes #
-
Eric W. Weisstein, “Halley’s method,” MathWorld, https://mathworld.wolfram.com/HalleysMethod.html ↩︎
-
Michael Levin, “Halley’s Method fractal art”, Forms of life, forms of mind, October 3, 2023, https://thoughtforms.life/halleys-method-fractal-art/ ↩︎