Introduction to complex numbers
This is not a math tutorial. See Why am I writing about math?
What is a complex number?
Real Numbers #
Not much needs to be said, they’re the numbers I’m used to: 0, 1, e, PI, -17.3, etc.
Imaginary numbers #
“We explored the idea of imaginary numbers” (I didn’t, I’ll make up for that here notes / Introduction to imaginary numbers
Imaginary numbers are multiples of the imaginary unit: i, -i, PIi, ei, etc.
Complex numbers #
The combination of real and imaginary numbers:
The number z in the example above can’t be simplified any more. The real part can’t be added to
the imaginary part.
You might see notation that looks like this:
Three main forms of complex numbers #
- Rectangular/Cartesian form:
- Polar form:
- Exponential form:
Where is the magnitude (distance from origin) and is the angle from the positive real axis.
The magnitude, modulus or absolute value of a complex number #
It seems that the terms magnitude, modulus, and absolute value are interchangeable. The magnitude or modulus of a complex number ( in the previous section’s example ) is the length of the line segment from the origin to the point on the complex plane.
It’s calculated with:
For the complex number :
Plotting complex numbers #
Plot the imaginary part on the vertical axis. Plot the imaginary part on the horizontal axis.
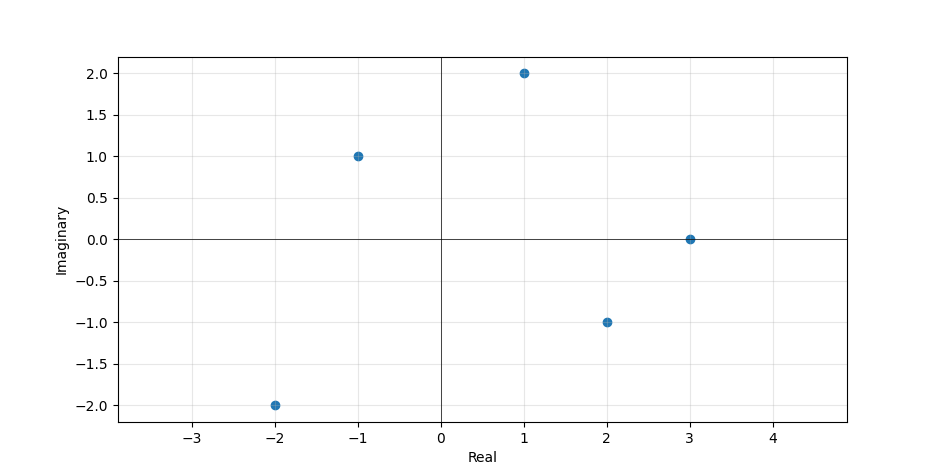
plotting complex numbers with pyplot
The code for generating the image above:
import matplotlib.pyplot as plt
import numpy as np
z = np.array([1 + 2j, -1 + 1j, 2 - 1j, -2 - 2j, 3 + 0j], dtype=np.complex64)
plt.scatter(z.real, z.imag)
plt.axhline(y=0, color="k", linewidth=0.5)
plt.axvline(x=0, color="k", linewidth=0.5)
plt.xlabel("Real")
plt.ylabel("Imaginary")
plt.grid(True, alpha=0.3)
plt.axis("equal")
plt.show()
Thinking about complex numbers #
Source: Claude, so proceed with caution.
Question: After a preamble about what I’m working on… “What are some intuitive approaches for thinking about the complex plane that might work for non-mathematicians”.
It’s just a 2D map #
Think of complex numbers as locations on a map. The real part is how far east/west you go, the
imaginary part is how far north/south. 3 + 2i is just “go 3 units right, 2 units up.”
(That’s how I do think about it, I’m trying to improve on that.)
Multiplication = rotation + stretching #
When you multiply by a complex number, you’re doing two things:
- rotating around the origin
- scaling (stretching or shrinking)
E.g., multiplying by i rotates everything 90 degrees counterclockwise. Multiply by i again
rotates another 90 degrees, etc. (See
notes / Introduction to imaginary numbers.
This seems to explain the significance of the sequence of the powers of i.)
More about complex numbers and rotation #
When you plot powers of i on the complex plane:
- i⁰ = 1 is at position (1, 0) — on the positive real axis
- i¹ = i is at position (0, 1) — rotated 90° counterclockwise
- i² = -1 is at position (-1, 0) — rotated another 90° (now 180° total)
- i³ = -i is at position (0, -1) — rotated another 90° (now 270° total)
- i⁴ = 1 is at position (1, 0) — rotated another 90° (full 360°, back to start)
Remember that 1 is also a complex number: 1 + 0i, that’s why it represents the point (1, 0) on
the complex plane. i is the complex number 0 + 1i, so it’s represented as (0, 1) on the
complex plane. Etc. Every real number is also a complex number with an imaginary part of zero. Every
imaginary number is also a complex number with a real part of zero.
Spirals everywhere #
(Related to the above section.)
Because multiplication combines rotation and scaling, when you repeatedly multiply a number by
itself (e.g., z, z^2, z^3, ...), you often get spirals. If the number is inside the unit circle
(less than 1(?)), it spirals inward. If it’s outside the unit circle, it spirals outward.
Two ways to describe a location #
Similar to how you could give the same directions as “go 3 blocks east, 4 blocks north”, or “walk 5 blocks at a 53 degree angle”, complex numbers can be written as:
- Rectangular:
a + bi(the x,y coordinates) - Polar: magnitude and angle (how far from origin, in which direction)
References #
Khan Academy. “Introduction to complex numbers | Imaginary and complex numbers | Precalculus | Khan Academy”. Feb 12, 2014. https://www.youtube.com/watch?v=SP-YJe7Vldo