Multiplying complex numbers

This is not a math tutorial. See Why am I writing about math?

The fast way:

a = complex(2, 3)
b = complex(4, 5)
z = a * b

print(z)
# (-7+22j)

Considering multiplication in terms of the rectangular form #

A complex number is any number that can be written as $a + bi$, where $i$ is the imaginary unit and $a$ and $b$ are real numbers.¹

Remember that $i = \sqrt(-1)$. Think about the process as though $i$ is a regular variable, for example $x$, but that the result of the multiplication needs to be in the form $a + bi$, not something like $ai^2 + bi$.

Multiplying a complex number by a scalar #

$a = 6+4i$:

$b = 3$

$b\cdot a = 3(6 + 4i) = 18 + 12i$

Multiplying a complex number by a complex number #

$a = 2+3i$

$b = 4+2i$

$a\cdot b = (2 + 3i)(4 + 2i) = 8 + 4i + 12i + 6i^2 = 8 + 16i - 6 = 2+16i$

Considering multiplication in terms of the polar form #

The polar coordinate system is outlined here: notes / The polar coordinate system

The polar coordinate system defines points on the complex plane in terms of a magnitude $r$ and an angle $\theta$. The angle $\theta$ determines how much the polar coordinate rotates away from the polar axis (the line starting from the center of the circle in the image below):

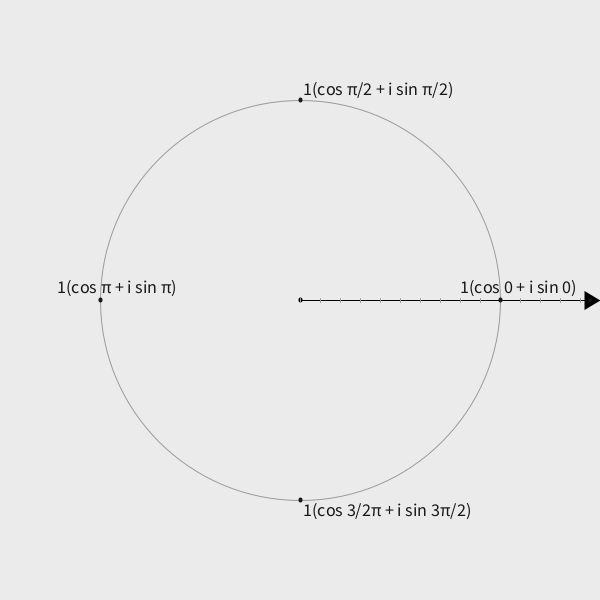
The polar form is essentially:

complex number = magnitude * (unit circle point at its angle)

See notes/ The polar coordinate system (where do the angles of for the powers of $i$ come from?)

Skipping the proof , the formula for multiplying complex numbers in polar form is:

The magnitudes of the numbers are multiplied and the angles are summed.

Polar form notation versus computation #

I’m not sure how better to phrase the issue. Polar form notation often represents complex numbers in the form:

This shows how the polar form related to the Cartesian (rectangular) form $a + bi$, but when working with complex numbers computationally, you don’t actually carry out the trig functions.

An example from Processing code:

class ComplexPolar {
  float r, theta, re, im;
  int hue;

  ComplexPolar(float r, float theta) {
    this.r = r;
    this.theta = theta;
    this.re = r * cos(theta);  // used in the sketch's code
    this.im = r * sin(theta);  // used in the sketch's code
    this.hue = (int)(theta * 180.0/PI) % 360;
  }

  ComplexPolar mult(ComplexPolar other) {
    return new ComplexPolar(
      r * other.r, theta + other.theta
      );
  }

  float magnitude() {
    return r;
  }
}

Multiplication of complex numbers on the unit circle #

When two complex numbers that are on the unit circle are multiplied, only the sine/cosine parts of the numbers are affected (because the magnitudes of the numbers are 1). This means that multiplication only has a rotation effect:

$i^0 \cdot i^1 = 1(cos\text{ }0 + i\text{ }sin\text{ }0)\times 1(cos\text{ }\pi/2 + i\text{ }sin\text{ }\pi/2)$

Multiplying a complex number by $i$ rotates the number 90 degrees counter-clockwise from the polar axis.

Multiplying a complex number 4 times by $i$ results in a 360 degree rotation (it’s back to the starting point).

Using complex numbers to parameterize the equation for a circle #

The way that multiplying complex numbers applies a rotation effect helps to explain how the formula for creating a circle can be parameterized.

The parameterized formula for a circle with radius $r$ centered at the origin is (in “cis” form):

The “cis” (cosine, imaginary, sine) notation expands to:

As $t$ varies from $0$ to $2\pi$, this traces a complete circle.

This is the way I’ve always drawn circles with Processing (ignoring the $i$ component):

float x = r*cos(t);
float y = r*sin(t);
t += PI/32 // or some other increment

Tracing what’s happening to points on the complex plane during the Mandelbrot iterations #

Related to Mandelbrot set (Processing)

I tried a small experiment with this here: notes / Tracing how numbers change during the Mandelbrot iterations

References #

Khan Academy. “Multiplying complex numbers.” Accessed on: January 26, 2026. https://www.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:complex/x2ec2f6f830c9fb89:complex-mul/a/multiplying-complex-numbers .