Print a Mandelbrot set to the console
Related to: notes / Mandelbrot set implemented with Processing. This is a slightly different implementation though.
A function to generate a Mandelbrot set:
import numpy as np
def mandelbrot_set(
real_values: np.ndarray[np.float64],
imag_values: np.ndarray[np.float64],
max_iterations: int,
) -> list[int]:
num_real = len(real_values)
num_imag = len(imag_values)
escape_counts = np.full((num_imag, num_real), max_iterations, dtype=int)
for i, imag in enumerate(imag_values):
for j, real in enumerate(real_values):
z = complex(0, 0)
c = complex(real, imag)
for iter in range(max_iterations):
if abs(z) > 2.0:
escape_counts[i][j] = iter
break
else:
z = z * z + c
return escape_counts
The function initializes a NumPy array with the value of max_iterations. Any complex numbers that
diverge before max_iterations have their iteration counts recorded in the array.
Any numbers that do not diverge before max_iterations are considered to be in the Mandelbrot set.
Note that this doesn’t prove that they are in the set. It’s possible that they would diverge given
more iterations.
The mandelbrot_set function can be called with:
real = np.linspace(-2, 0.5, 20)
imag = np.linspace(1.25, -1.25, 20)
max_iterations = 50
result = mandelbrot_set(real, imag, max_iterations)
print(result)
Example call
❯ python mandelbrot.py
[[ 1 1 1 1 2 2 2 2 3 3 3 3 3 3 3 3 2 2 2 2]
[ 1 1 1 2 2 2 3 3 3 3 3 3 4 4 6 4 3 3 2 2]
[ 1 1 2 2 3 3 3 3 3 3 4 4 4 5 9 19 4 4 3 3]
[ 1 1 2 3 3 3 3 3 3 4 4 4 5 26 19 11 5 4 4 3]
[ 1 1 3 3 3 3 3 3 4 4 5 7 7 10 50 50 8 6 5 3]
[ 1 2 3 3 3 3 3 4 5 5 6 25 50 50 50 50 50 13 28 4]
[ 1 3 3 3 3 4 6 5 5 6 25 50 50 50 50 50 50 50 9 5]
[ 1 3 4 4 5 6 12 10 10 9 50 50 50 50 50 50 50 50 50 6]
[ 1 4 4 5 5 7 15 50 50 38 50 50 50 50 50 50 50 50 50 5]
[ 1 5 7 6 8 45 50 50 50 50 50 50 50 50 50 50 50 50 9 5]
[ 1 5 7 6 8 45 50 50 50 50 50 50 50 50 50 50 50 50 9 5]
[ 1 4 4 5 5 7 15 50 50 38 50 50 50 50 50 50 50 50 50 5]
[ 1 3 4 4 5 6 12 10 10 9 50 50 50 50 50 50 50 50 50 6]
[ 1 3 3 3 3 4 6 5 5 6 25 50 50 50 50 50 50 50 9 5]
[ 1 2 3 3 3 3 3 4 5 5 6 25 50 50 50 50 50 13 28 4]
[ 1 1 3 3 3 3 3 3 4 4 5 7 7 10 50 50 8 6 5 3]
[ 1 1 2 3 3 3 3 3 3 4 4 4 5 26 19 11 5 4 4 3]
[ 1 1 2 2 3 3 3 3 3 3 4 4 4 5 9 19 4 4 3 3]
[ 1 1 1 2 2 2 3 3 3 3 3 3 4 4 6 4 3 3 2 2]
[ 1 1 1 1 2 2 2 2 3 3 3 3 3 3 3 3 2 2 2 2]]
The pattern defined by the value 50 is a small approximation of the Mandelbrot set.
Styling the output with Textualize/Rich #
“Rich is a Python library for rich text and beautiful formatting in the terminal.”1
A quick example:
import numpy as np
from rich import print
from rich.panel import Panel
from rich import box
# ... same mandelbrot_set definition as in the code above
real = np.linspace(-2, 0.5, 20)
imag = np.linspace(1.25, -1.25, 20)
max_iterations = 50
result = mandelbrot_set(real, imag, max_iterations)
mandelbrot_repr = ""
for row in result:
row_repr = ""
for count in row:
count_str = str(count)
countstr_len = len(count_str)
for char in range(4 - countstr_len):
count_str += " "
if count == max_iterations: # allows for setting a specific color for the set
color_code = 129
style = "bold"
else:
color_code = count
style = "bold"
# it's convenient that standard terminal color codes can be used:
count_str = (
f"[color({color_code}) {style}]{count_str}[/color({color_code}) {style}]"
)
row_repr += count_str
mandelbrot_repr += f"{row_repr}\n"
print(Panel(mandelbrot_repr, title="Mandelbrot set", expand=False, box=box.DOUBLE_EDGE))
Output in the terminal (the colors aren’t preserved when copied and pasted to this note):
╔═════════════════════════════════ Mandelbrot set ═════════════════════════════════╗
║ 1 1 1 1 2 2 2 2 3 3 3 3 3 3 3 3 2 2 2 2 ║
║ 1 1 1 2 2 2 3 3 3 3 3 3 4 4 6 4 3 3 2 2 ║
║ 1 1 2 2 3 3 3 3 3 3 4 4 4 5 9 19 4 4 3 3 ║
║ 1 1 2 3 3 3 3 3 3 4 4 4 5 26 19 11 5 4 4 3 ║
║ 1 1 3 3 3 3 3 3 4 4 5 7 7 10 50 50 8 6 5 3 ║
║ 1 2 3 3 3 3 3 4 5 5 6 25 50 50 50 50 50 13 28 4 ║
║ 1 3 3 3 3 4 6 5 5 6 25 50 50 50 50 50 50 50 9 5 ║
║ 1 3 4 4 5 6 12 10 10 9 50 50 50 50 50 50 50 50 50 6 ║
║ 1 4 4 5 5 7 15 50 50 38 50 50 50 50 50 50 50 50 50 5 ║
║ 1 5 7 6 8 45 50 50 50 50 50 50 50 50 50 50 50 50 9 5 ║
║ 1 5 7 6 8 45 50 50 50 50 50 50 50 50 50 50 50 50 9 5 ║
║ 1 4 4 5 5 7 15 50 50 38 50 50 50 50 50 50 50 50 50 5 ║
║ 1 3 4 4 5 6 12 10 10 9 50 50 50 50 50 50 50 50 50 6 ║
║ 1 3 3 3 3 4 6 5 5 6 25 50 50 50 50 50 50 50 9 5 ║
║ 1 2 3 3 3 3 3 4 5 5 6 25 50 50 50 50 50 13 28 4 ║
║ 1 1 3 3 3 3 3 3 4 4 5 7 7 10 50 50 8 6 5 3 ║
║ 1 1 2 3 3 3 3 3 3 4 4 4 5 26 19 11 5 4 4 3 ║
║ 1 1 2 2 3 3 3 3 3 3 4 4 4 5 9 19 4 4 3 3 ║
║ 1 1 1 2 2 2 3 3 3 3 3 3 4 4 6 4 3 3 2 2 ║
║ 1 1 1 1 2 2 2 2 3 3 3 3 3 3 3 3 2 2 2 2 ║
║ ║
╚══════════════════════════════════════════════════════════════════════════════════╝

Here’s a 40x40 set with the same max_iterations count (50) as in the previous image:
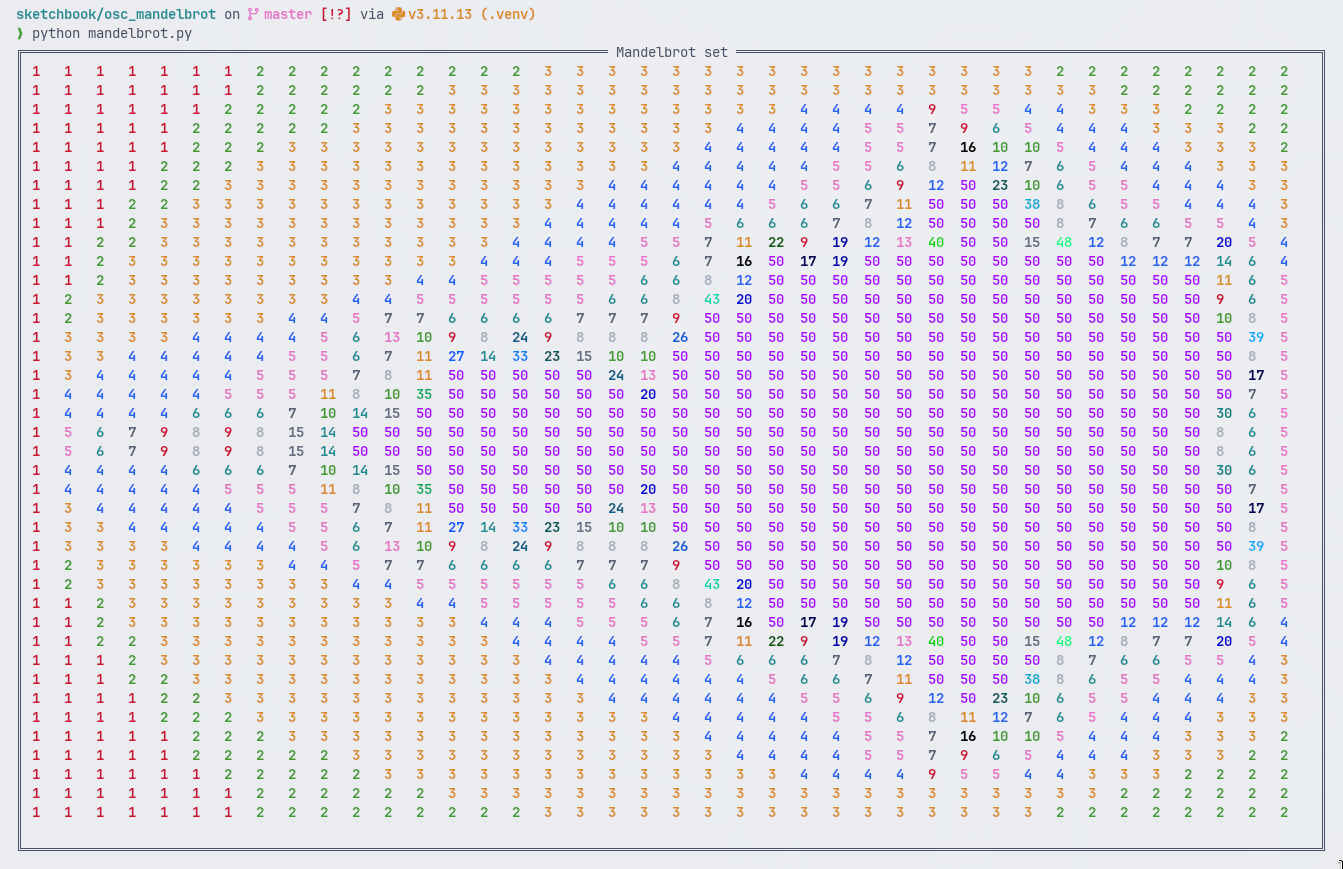
The iteration counts are easier to read in the plain text version:
╔═════════════════════════════════════════════════════════════════════════ Mandelbrot set ═════════════════════════════════════════════════════════════════════════╗
║ 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 ║
║ 1 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 ║
║ 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 9 5 5 4 4 3 3 3 2 2 2 2 ║
║ 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 5 5 7 9 6 5 4 4 4 3 3 3 2 2 ║
║ 1 1 1 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5 7 16 10 10 5 4 4 4 3 3 3 2 ║
║ 1 1 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5 6 8 11 12 7 6 5 4 4 4 3 3 3 ║
║ 1 1 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 5 5 6 9 12 50 23 10 6 5 5 4 4 4 3 3 ║
║ 1 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 5 6 6 7 11 50 50 50 38 8 6 5 5 4 4 4 3 ║
║ 1 1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 6 6 6 7 8 12 50 50 50 50 8 7 6 6 5 5 4 3 ║
║ 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 5 5 7 11 22 9 19 12 13 40 50 50 15 48 12 8 7 7 20 5 4 ║
║ 1 1 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 6 7 16 50 17 19 50 50 50 50 50 50 50 50 12 12 12 14 6 4 ║
║ 1 1 2 3 3 3 3 3 3 3 3 3 4 4 5 5 5 5 5 6 6 8 12 50 50 50 50 50 50 50 50 50 50 50 50 50 50 11 6 5 ║
║ 1 2 3 3 3 3 3 3 3 3 4 4 5 5 5 5 5 5 6 6 8 43 20 50 50 50 50 50 50 50 50 50 50 50 50 50 50 9 6 5 ║
║ 1 2 3 3 3 3 3 3 4 4 5 7 7 6 6 6 6 7 7 7 9 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 10 8 5 ║
║ 1 3 3 3 3 4 4 4 4 5 6 13 10 9 8 24 9 8 8 8 26 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 39 5 ║
║ 1 3 3 4 4 4 4 4 5 5 6 7 11 27 14 33 23 15 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8 5 ║
║ 1 3 4 4 4 4 4 5 5 5 7 8 11 50 50 50 50 50 24 13 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 17 5 ║
║ 1 4 4 4 4 4 5 5 5 11 8 10 35 50 50 50 50 50 50 20 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 7 5 ║
║ 1 4 4 4 4 6 6 6 7 10 14 15 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 30 6 5 ║
║ 1 5 6 7 9 8 9 8 15 14 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8 6 5 ║
║ 1 5 6 7 9 8 9 8 15 14 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8 6 5 ║
║ 1 4 4 4 4 6 6 6 7 10 14 15 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 30 6 5 ║
║ 1 4 4 4 4 4 5 5 5 11 8 10 35 50 50 50 50 50 50 20 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 7 5 ║
║ 1 3 4 4 4 4 4 5 5 5 7 8 11 50 50 50 50 50 24 13 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 17 5 ║
║ 1 3 3 4 4 4 4 4 5 5 6 7 11 27 14 33 23 15 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8 5 ║
║ 1 3 3 3 3 4 4 4 4 5 6 13 10 9 8 24 9 8 8 8 26 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 39 5 ║
║ 1 2 3 3 3 3 3 3 4 4 5 7 7 6 6 6 6 7 7 7 9 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 10 8 5 ║
║ 1 2 3 3 3 3 3 3 3 3 4 4 5 5 5 5 5 5 6 6 8 43 20 50 50 50 50 50 50 50 50 50 50 50 50 50 50 9 6 5 ║
║ 1 1 2 3 3 3 3 3 3 3 3 3 4 4 5 5 5 5 5 6 6 8 12 50 50 50 50 50 50 50 50 50 50 50 50 50 50 11 6 5 ║
║ 1 1 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 6 7 16 50 17 19 50 50 50 50 50 50 50 50 12 12 12 14 6 4 ║
║ 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 5 5 7 11 22 9 19 12 13 40 50 50 15 48 12 8 7 7 20 5 4 ║
║ 1 1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 6 6 6 7 8 12 50 50 50 50 8 7 6 6 5 5 4 3 ║
║ 1 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 5 6 6 7 11 50 50 50 38 8 6 5 5 4 4 4 3 ║
║ 1 1 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 5 5 6 9 12 50 23 10 6 5 5 4 4 4 3 3 ║
║ 1 1 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5 6 8 11 12 7 6 5 4 4 4 3 3 3 ║
║ 1 1 1 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5 7 16 10 10 5 4 4 4 3 3 3 2 ║
║ 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 5 5 7 9 6 5 4 4 4 3 3 3 2 2 ║
║ 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 9 5 5 4 4 3 3 3 2 2 2 2 ║
║ 1 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 ║
║ 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 ║
║ ║
╚══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
It’s interesting to look at how what’s considered to be in the set changes if the max_iterations
value is pushed up to 200:
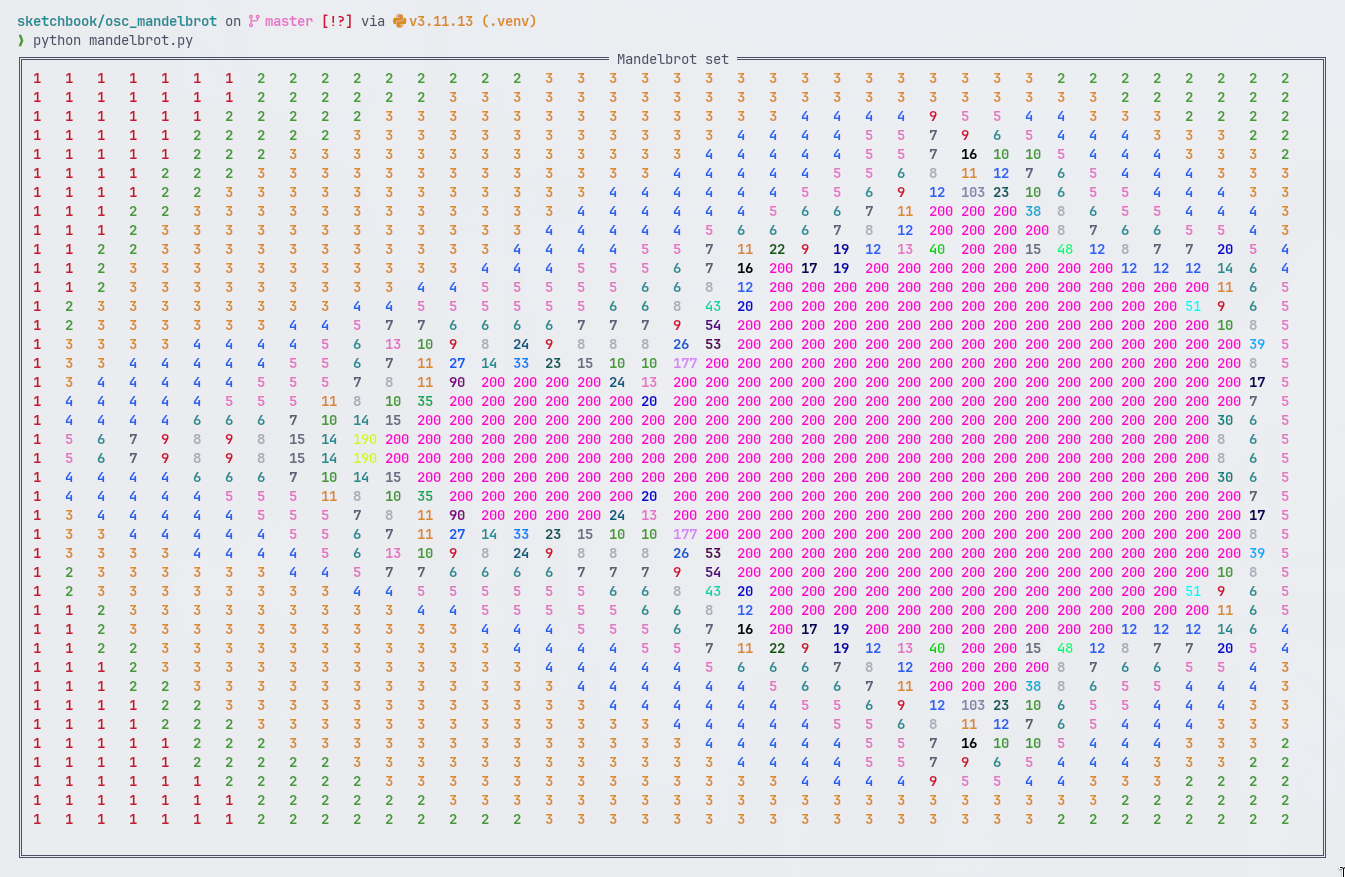
Raw text output:
╔═════════════════════════════════════════════════════════════════════════ Mandelbrot set ═════════════════════════════════════════════════════════════════════════╗
║ 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 ║
║ 1 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 ║
║ 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 9 5 5 4 4 3 3 3 2 2 2 2 ║
║ 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 5 5 7 9 6 5 4 4 4 3 3 3 2 2 ║
║ 1 1 1 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5 7 16 10 10 5 4 4 4 3 3 3 2 ║
║ 1 1 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5 6 8 11 12 7 6 5 4 4 4 3 3 3 ║
║ 1 1 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 5 5 6 9 12 103 23 10 6 5 5 4 4 4 3 3 ║
║ 1 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 5 6 6 7 11 200 200 200 38 8 6 5 5 4 4 4 3 ║
║ 1 1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 6 6 6 7 8 12 200 200 200 200 8 7 6 6 5 5 4 3 ║
║ 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 5 5 7 11 22 9 19 12 13 40 200 200 15 48 12 8 7 7 20 5 4 ║
║ 1 1 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 6 7 16 200 17 19 200 200 200 200 200 200 200 200 12 12 12 14 6 4 ║
║ 1 1 2 3 3 3 3 3 3 3 3 3 4 4 5 5 5 5 5 6 6 8 12 200 200 200 200 200 200 200 200 200 200 200 200 200 200 11 6 5 ║
║ 1 2 3 3 3 3 3 3 3 3 4 4 5 5 5 5 5 5 6 6 8 43 20 200 200 200 200 200 200 200 200 200 200 200 200 200 51 9 6 5 ║
║ 1 2 3 3 3 3 3 3 4 4 5 7 7 6 6 6 6 7 7 7 9 54 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 10 8 5 ║
║ 1 3 3 3 3 4 4 4 4 5 6 13 10 9 8 24 9 8 8 8 26 53 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 39 5 ║
║ 1 3 3 4 4 4 4 4 5 5 6 7 11 27 14 33 23 15 10 10 177 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 8 5 ║
║ 1 3 4 4 4 4 4 5 5 5 7 8 11 90 200 200 200 200 24 13 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 17 5 ║
║ 1 4 4 4 4 4 5 5 5 11 8 10 35 200 200 200 200 200 200 20 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 7 5 ║
║ 1 4 4 4 4 6 6 6 7 10 14 15 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 30 6 5 ║
║ 1 5 6 7 9 8 9 8 15 14 190 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 8 6 5 ║
║ 1 5 6 7 9 8 9 8 15 14 190 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 8 6 5 ║
║ 1 4 4 4 4 6 6 6 7 10 14 15 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 30 6 5 ║
║ 1 4 4 4 4 4 5 5 5 11 8 10 35 200 200 200 200 200 200 20 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 7 5 ║
║ 1 3 4 4 4 4 4 5 5 5 7 8 11 90 200 200 200 200 24 13 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 17 5 ║
║ 1 3 3 4 4 4 4 4 5 5 6 7 11 27 14 33 23 15 10 10 177 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 8 5 ║
║ 1 3 3 3 3 4 4 4 4 5 6 13 10 9 8 24 9 8 8 8 26 53 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 39 5 ║
║ 1 2 3 3 3 3 3 3 4 4 5 7 7 6 6 6 6 7 7 7 9 54 200 200 200 200 200 200 200 200 200 200 200 200 200 200 200 10 8 5 ║
║ 1 2 3 3 3 3 3 3 3 3 4 4 5 5 5 5 5 5 6 6 8 43 20 200 200 200 200 200 200 200 200 200 200 200 200 200 51 9 6 5 ║
║ 1 1 2 3 3 3 3 3 3 3 3 3 4 4 5 5 5 5 5 6 6 8 12 200 200 200 200 200 200 200 200 200 200 200 200 200 200 11 6 5 ║
║ 1 1 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 6 7 16 200 17 19 200 200 200 200 200 200 200 200 12 12 12 14 6 4 ║
║ 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 5 5 7 11 22 9 19 12 13 40 200 200 15 48 12 8 7 7 20 5 4 ║
║ 1 1 1 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 6 6 6 7 8 12 200 200 200 200 8 7 6 6 5 5 4 3 ║
║ 1 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 5 6 6 7 11 200 200 200 38 8 6 5 5 4 4 4 3 ║
║ 1 1 1 1 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 5 5 6 9 12 103 23 10 6 5 5 4 4 4 3 3 ║
║ 1 1 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5 6 8 11 12 7 6 5 4 4 4 3 3 3 ║
║ 1 1 1 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 5 5 7 16 10 10 5 4 4 4 3 3 3 2 ║
║ 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 5 5 7 9 6 5 4 4 4 3 3 3 2 2 ║
║ 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 9 5 5 4 4 3 3 3 2 2 2 2 ║
║ 1 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 ║
║ 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 ║
║ ║
╚══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╝
For fun, here’s a 50x50 set with the spaces removed around three digit iteration counts so that it renders close to the actual proportions of the real and imaginary domains:

-
Textualize/rich README, “rich,” Accessed on: January 25, 2026, https://github.com/Textualize/rich . ↩︎