Real and complex numbers in space

This is not a math tutorial. See Why am I writing about math?

Real numbers ($R$) are numbers that exist on the number line.

Understanding dimensions

The physical world has three dimensions.

A sheet of graph paper (ignoring its thickness) is conceptually a two dimensional object.

A number line is a 1 dimensional object.

To describe a point on the number line only requires a single coordinate.

To describe a point on a Cartesian plane requires two coordinates.

To describe a point in space requires three coordinates.

The dimensionality of an object could be considered as the degrees of freedom that the object has.

Complex numbers are two dimensional

Complex numbers (numbers in the form $a + bi$) can be represented a points on the complex plane. The complex plane maps to a 2D Cartesian plane. The horizontal x-axis represents the real part of a complex number. The vertical y-axis represents the imaginary part of the complex number.

See notes / Introduction to imaginary numbers

Visualizing complex numbers

The following code creates a 10x10 grid of complex numbers, with the real plane in the range (-1, 1) and the real part of the complex plane also in the range (-1, 1):

import numpy as np
import matplotlib.pyplot as plt

xmin = -1.0
xmax = 1.0
ymin = -1.0
ymax = 1.0
width = 10
height = 10


x = np.linspace(xmin, xmax, width)
y = np.linspace(ymin, ymax, height)
X, Y = np.meshgrid(x, y)
Z = X + 1j * Y

# Scatter plot the points on the complex plane
plt.scatter(Z.real, Z.imag)
plt.xlabel("Real")
plt.ylabel("Imaginary")
plt.axis("equal")
plt.grid(True)
plt.show()

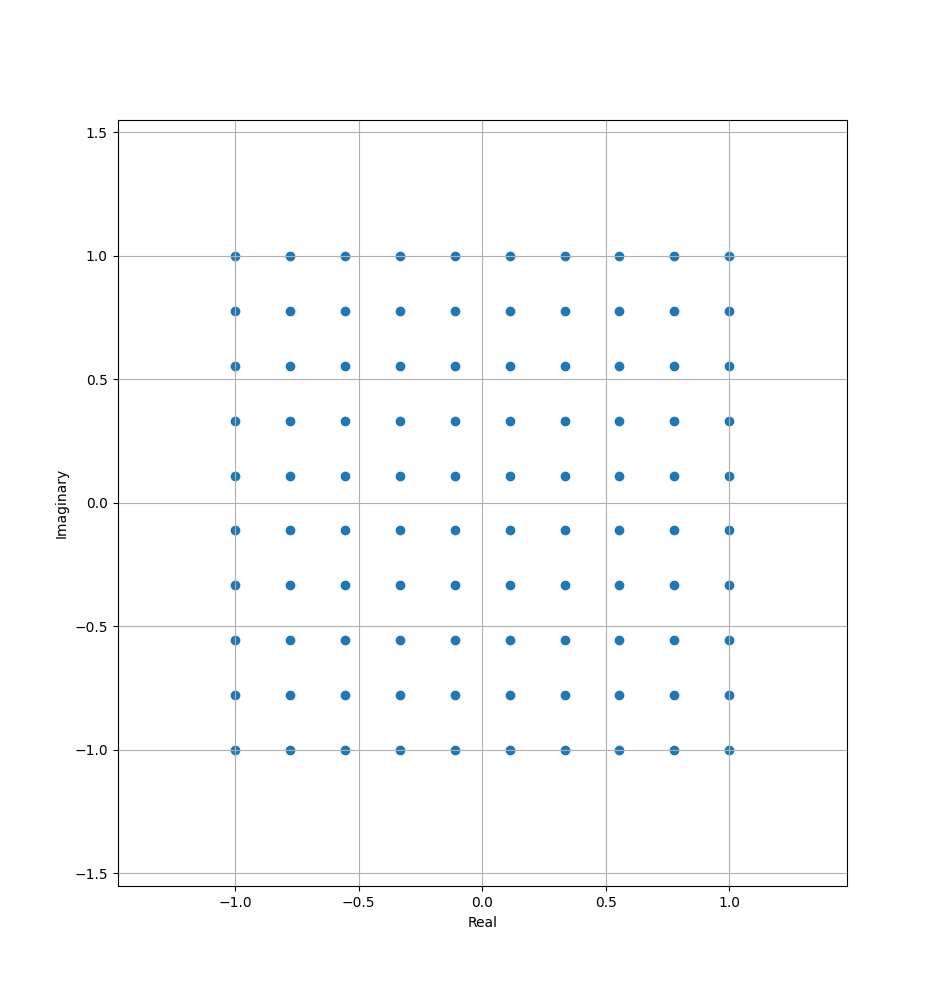
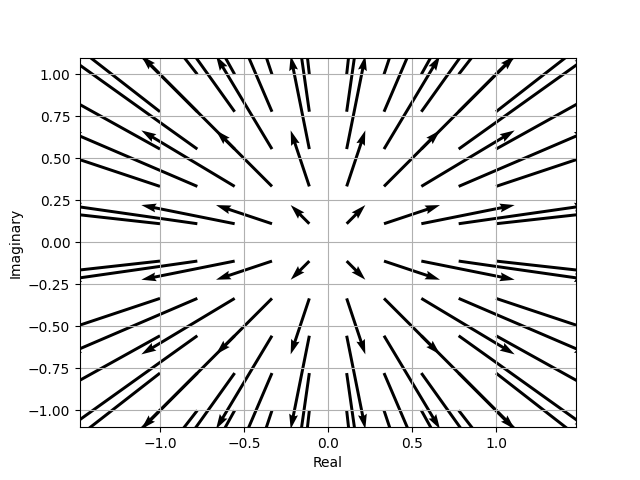
Complex numbers can be visualized as vectors.

# A quiver plot is a 2D graph that displays a field of vectors as arrows.
# quiver([X, Y], U, V, [C], /, **kwargs)
# X, Y define the arrow locations, U, V define the arrow directions.
# The `angles` arg sets the direction of the arrows; "xy": arrows point from (x, y) to
# (x+u, y+v)
plt.quiver(
    Z.real,  # arrow X coordinate start
    Z.imag,  # arrow Y coordinage start; the r part of the imaginary number
    Z.real,  # point arrows in the direction of the complex number
    Z.imag,  # point arrows in the direction of the complex number
    angles="xy",
    scale_units="xy",
    scale=1,
)

Here’s a scaled down version of the complex numbers that are being used in these examples. It’s a 4x4 grid instead of a 10x10 grid:

 [[-1.        -1.j         -0.33333333-1.j          0.33333333-1.j        1.        -1.j        ]
 [-1.        -0.33333333j -0.33333333-0.33333333j  0.33333333-0.33333333j 1.        -0.33333333j]
 [-1.        +0.33333333j -0.33333333+0.33333333j  0.33333333+0.33333333j 1.        +0.33333333j]
 [-1.        +1.j         -0.33333333+1.j          0.33333333+1.j         1.        +1.j        ]]

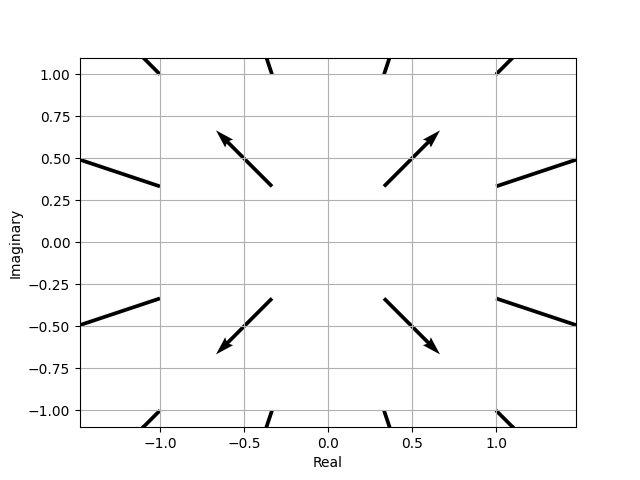
Calculating the angle for a complex number (also called the argument or phase)

Starting from a complex number in the rectangular form: -0.33333333-1.j

Identify the components:

• real part: -0.33333333
• imaginary part: -1.0

The number is a + bi = -0.33333333-1j

Visualize (imagine for now) the number on the complex plane:

x = -0.33333333, y = -1.0. The number is in the third quadrant, both x and y are negative.

Calculate the angle of the point:

The simple approach with Python is theta = np.arctan2(y, x), or theta = np.angle(-0.33333333-1j)

In [10]: np.angle(-0.33333333-1j)  #   np.float64(-1.8925468781915389)
Out[10]: np.arctan2(-1, 0.33333333)  # np.float64(-1.8925468781915389)

Note that np.angle returns the angle of a complex number in radians, np.arctan2 returns the angle of (opposite, adjacent), (x, y), (real, imag).

Related

• notes / Solving polynomial equations > solving polynomial equations for complex roots