Solve cosine of pi over four
This is not a math tutorial. See Why am I writing about math?
Related to converting complex numbers from the polar to the rectalinear form: notes / Polynomial functions.
The value of is derived from the properties of a 45-45-90 degree right angle triangle.
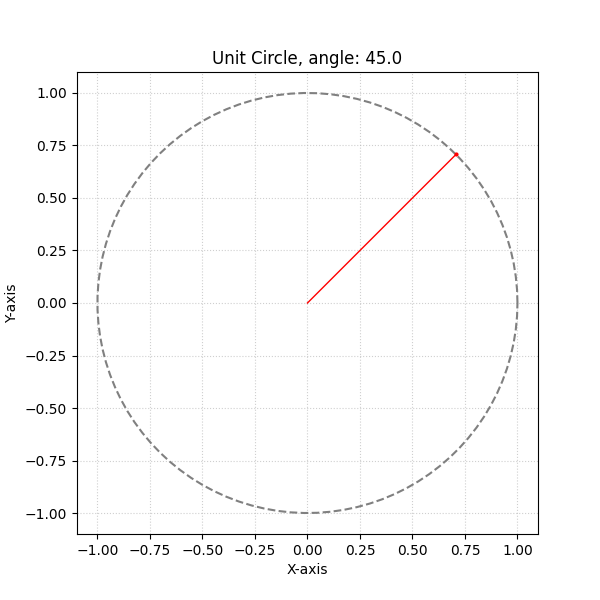
Looking at the image above, imagine that it forms a right-angle triangle, with point A at (0, 0), point B where the angle (hypotenuse) touches the circle and point D where a line that descends straight down (parallel to the x=0 line) from point B, touches the y=0 line. A better way of describing the line from point B is that “we’ve dropped a perpendicular from point B”.
So we’ve got a conceptual right angle triangle. The angle at point D is 90 degrees, the angle at point A is or 45 degrees, and the angle at B is unknown.
My motivation here is to solve , but other things may get figured out along the way.
What’s the measure (in radians) of angle ABD? #
Angle ABD is the angle of the point that touches the circle. The sum of the angles of a triangle add
up to 180 degrees. 180 degrees is PI radians. So the angle ABD should be
PI - PI/2 + PI/4 = (4PI - 2PI - PI)/4 = PI/4
Calculate the lengths of the sides of a right angle triangle on the unit circle #
We know that the hypotenuse has a length of 1.
Since angles ABD and DAB have are the same, we know that the lines AB and AD have the same length. It’s an isosceles triangle (not an equilateral triangle).
The sides can be figured out with the Pythagorean theorem: a^2 + b^2 = c^2, but also, since a = b,
we can use 2a^2 = 1.
I’ll just call the sides :
To remove the square root from the denominator:
So the lengths of the sides are:
- a:
- b:
- c:
Calculate the sine, cosine, and tangent of PI/4 radians #
The cosine of PI/4 radians is the x coordinate of the point on the unit circle.
The sine of PI/4 radians is the y coordinate of the point on the unit circle.
The x coordinate is . The y coordinate is also .
To answer the question that motivated writing this note, the cosine of PI/4 radians is .
What is the tangent of PI/4 radians?
Since the sine and cosine values are equal, the tangent simplifies to:
Remember what tangent means. The tangent of an angle is the slope of the line. It makes sense that the tangent of an isosceles triangle is 1 — as we move along the line, for every change in x there’s an equal change in y.
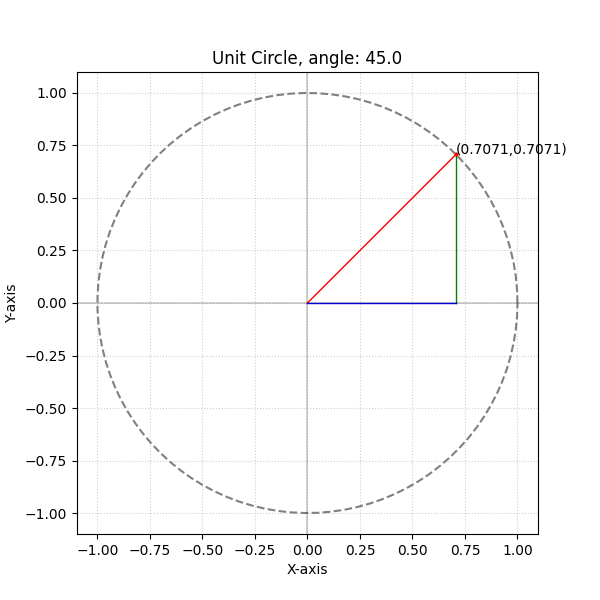
Generated by second code example
Unit circle Python code #
A quick Python script to draw a unit circle with an angle. By the end of writing this note I might know how to draw the point that falls on the x-axis (point D).
import numpy as np
import matplotlib.pyplot as plt
def plot_unit_circle_with_angle(angle_rad):
_, ax = plt.subplots(figsize=(6, 6))
theta = np.linspace(0, 2 * np.pi, 100)
x = np.cos(theta)
y = np.sin(theta)
ax.plot(x, y, color="gray", linestyle="--", label="Unit Circle")
x_angle = np.cos(angle_rad)
y_angle = np.sin(angle_rad)
ax.plot(
[0, x_angle],
[0, y_angle],
color="red",
linewidth=1,
)
ax.plot(x_angle, y_angle, "ro", markersize=2)
ax.set_aspect("equal", adjustable="box")
ax.set_xlabel("X-axis")
ax.set_ylabel("Y-axis")
ax.set_title(f"Unit Circle, angle: {np.degrees(angle_rad)}")
ax.grid(True, linestyle=":", alpha=0.6)
plt.show()
plot_unit_circle_with_angle(np.pi / 4)
Improved code:
import numpy as np
import matplotlib.pyplot as plt
def plot_unit_circle_with_angle(angle_rad):
_, ax = plt.subplots(figsize=(6, 6))
theta = np.linspace(0, 2 * np.pi, 100)
x = np.cos(theta)
y = np.sin(theta)
ax.plot(x, y, color="gray", linestyle="--", label="Unit Circle")
x_angle = np.cos(angle_rad)
y_angle = np.sin(angle_rad)
# NOTE: lists of ax.plot args seem to work differently than I expected
# first list is x values, second list is y values (?)
ax.plot(
[0, x_angle],
[0, y_angle],
color="red",
linewidth=1,
)
ax.plot(
[x_angle, x_angle],
[y_angle, 0],
color="green",
linewidth=1,
)
ax.plot(
[0, x_angle],
[0, 0],
color="blue",
linewidth=1,
)
ax.plot(x_angle, y_angle, "ro", label=f"{x_angle},{y_angle}", markersize=2)
ax.annotate(f"({x_angle:.4f},{y_angle:.4f})", xy=(x_angle, y_angle))
ax.set_aspect("equal", adjustable="box")
ax.set_xlabel("X-axis")
ax.set_ylabel("Y-axis")
ax.set_title(f"Unit Circle, angle: {np.degrees(angle_rad)}")
ax.grid(True, linestyle=":", alpha=0.6)
ax.axhline(y=0, color="k", linewidth=0.25)
ax.axvline(x=0, color="k", linewidth=0.25)
plt.show()
plot_unit_circle_with_angle(np.pi / 4)
References #
Kahn Academy. Solving triangle in unit circle | Trigonometry | Khan Academy. Mar 28, 2014. https://www.youtube.com/watch?v=KoYZErFpZ5Q