The polar coordinate system

This is not a math tutorial. See Why am I writing about math?

The Wikipedia Polar coordinate system page seems especially good (accessed on January 19, 2026).

Note: there’s some useful content starting at the heading: Writing complex numbers in the polar form

The polar coordinate system uses distance and angle to indicate where a point is on a 2D plane:

• distance: the point’s distance from the pole
• angle: the point’s direction from the pole, relative to the direction of the polar axis

Polar coordinates are written as $(r, \theta)$ as opposed to $(x, y)$ with the Cartesian system.

Polar coordinates have a pole that acts like the origin in the Cartesian system, and an axis that acts like the x-axis in the Cartesian system. Except the polar axis has a starting point ($0$) that is treated like an origin.

• the $r$ component of a polar coordinate is the distance from the origin.
• the $\theta$ component of a polar coordinate is the angle from the polar axis

Positive angles are measured counter-clockwise from the polar axis. Negative angles are measured counter clockwise from the polar axis.

Can $r$ be negative? My understanding is that $r$ is the magnitude and is always positive, but it seems that $-r$ is a reflection — $-r\theta$ is $180^\circ$ from $r\theta$.

Writing complex numbers in the polar form #

The form that seems clearest to me is $r\cdot(\cos(\theta) + i\cdot\sin(\theta))$.

It can also be written without explicit multiplication: $r(\cos \theta + i \sin\theta)$ There’s also a shorthand notation where cis stands for “cosine + i sine”: $r\cdot cis(\theta)$

There is also a form of writing complex numbers using the angle ($\angle$) symbol: $r\angle\theta$ means “magnitude r at angle $\theta$”.

The exponential form of complex numbers #

I’m ignoring the exponential form for now.

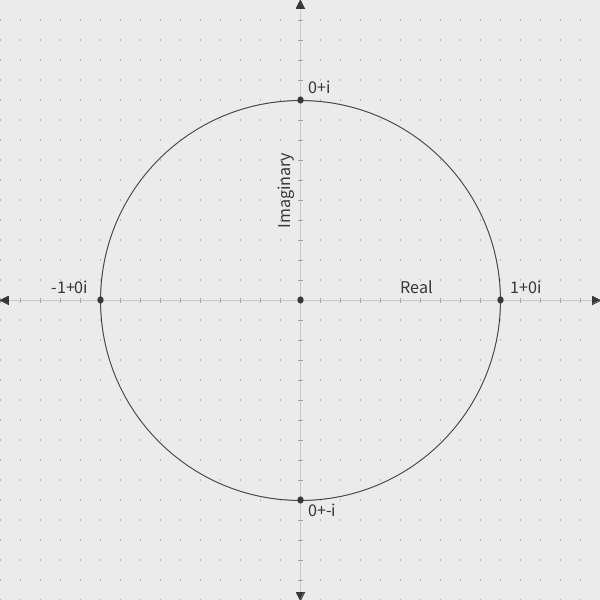
The rectangular form of the powers of i #

It’s useful to look at a plot of the powers of $i$ in the rectangular form to see how the angles for the polar form are derived

The powers of $i$ in the rectangular form:

• $i^0 = 1 + 0i$
• $i^1 = 0 + i$
• $i^2 = -1 + 0i$
• i^3 = 0 + -i$

The powers of i in the polar form #

• $i^0 = 1(cos 0 + i sin 0) = 1(1 + i\cdot 0) = 1$
• $i^1 = 1(cos \pi/2 + i sin \pi/2) = 1(0 + i\cdot 1) = i$
• $i^2 = 1(cos \pi + i sin \pi) = 1(-1 i\cdot 0) = -1$
• $i^3 = 1(cos 3\pi/2 + i sin 3\pi/2) = 1(0 + i\cdot(-1)) = -i$

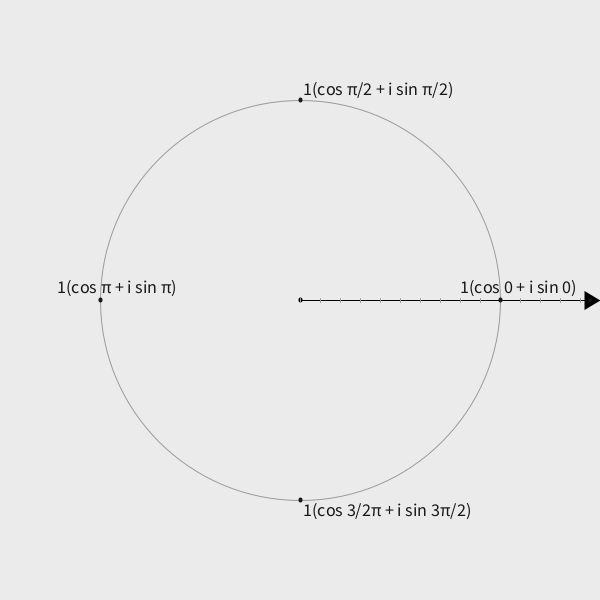
Where do the angles for the powers of i come from? #

Looking at the rectangular complex plane, it’s obvious that the angles can be calculated using the rules of trigonometry based on the real and imaginary components of the powers of $i$. But I think a better answer is that the angles are what they are by definition:

$i$ is defined as the square root of $-1$: $i^2 = -1$. This creates a system that has certain characteristics:

1. start with algebra: We want $i^2 = -1$
2. rectangular form: We define $i = 0 + 1i$, so it plots at (0, 1)
3. convert to polar: the point (0, 1) is at distance 1, angle $\pi/2$

So the angle $\pi/2$ [comes from the] requirement that:

• $i$ is purely imaginary (real part = 0)
• $i$ has a magnitude 1 (on the unit circle)
• $i^2 = -1$ (the defining property) ¹

This explains why $i^2 = -1$ makes sense in terms of geometry. See notes / Multiplying complex numbers

References #

Wikipedia contributors. “Polar coordinate system.” Accessed on: January 19, 2026. https://en.wikipedia.org/wiki/Polar_coordinate_system#Complex_numbers .

Professor Leonard. “Introduction to Polar Coordinates (Precalculus - Trigonometry 36).” Nov 18, 2021. https://www.youtube.com/watch?v=Ol_a6LEdo3M .